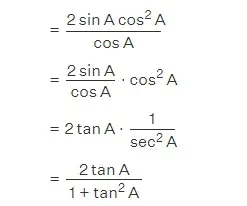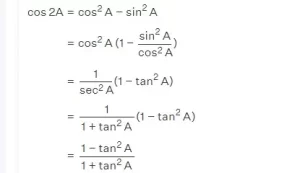Ángulo doble
sin (A + B) = sin A cos B + cos A sin B
cos (A + B) = cos A cos B - sin A sin B
tan (A + B) = (tan A + tan B) / (1 - tan A tan B)
¿Qué son las fórmulas del ángulo doble?
Derivaremos las fórmulas de ángulo doble de sin, cos y tan sustituyendo A = B en cada una de las fórmulas de suma anteriores. Además, derivaremos algunas fórmulas alternativas utilizando las identidades pitagóricas. Aquí están las fórmulas de los ángulos dobles seguidas de la derivación de cada fórmula.
Fórmulas de ángulos dobles de sin, cos y tan
Las fórmulas del ángulo doble de sin, cos y tan son,
sin 2A = 2 sin A cos A (o) (2 tan A) / (1 + tan2A)
cos 2A = cos2A - sin2A (o) 2cos2A - 1 (o) 1 - 2sin2A (o) (1 - tan2A) / (1 + tan2A)
tan 2A = (2 tan A) / (1 - tan2A)
Derivación de las fórmulas del ángulo doble
Vamos a derivar la(s) fórmula(s) del ángulo doble de cada uno de los sin, cos y tan uno por uno.
Fórmulas del doble ángulo de Sin
La fórmula de la suma de la función seno es
sin (A + B) = sin A cos B + cos A sin B
Cuando A = B, la fórmula anterior se convierte en
sin (A + A) = sin A cos A + cos A sin A
sin 2A = 2 sin A cos A
Derivemos una fórmula alternativa para sen 2A en términos de tan utilizando la identidad pitagórica sec2A = 1 + tan2A.
sin 2 A = 2 sin A cos A
Así, las fórmulas del doble ángulo de la función seno son
sin 2A = 2 sin A cos A (o) (2 tan A) / (1 + tan2A)
Fórmulas del doble ángulo del cos
La fórmula de la suma de la función coseno es
cos (A + B) = cos A cos B - sin A sin B
Cuando A = B, la fórmula anterior se convierte en
cos (A + A) = cos A cos A - sin A sin A
cos 2A = cos2A - sin2A
Usemos esto como fórmula base para derivar otras dos fórmulas de cos 2A usando la identidad pitagórica sin2A + cos2A = 1.
(i) cos 2A = cos2A - (1 - cos2A) = 2cos2A - 1
(ii) cos 2A = (1- sin2A) - sin2A = 1 - 2sin2A
Ahora, derivaremos la fórmula de cos 2A en términos de tan utilizando la fórmula base.
Así, las fórmulas del doble ángulo de la función coseno son
cos 2A = cos2A - sin2A (o) 2cos2A - 1 (o) 1 - 2sin2A (o) (1 - tan2A) / (1 + tan2A)
Fórmulas de doble ángulo de Tan
La fórmula de la suma de la función tangente es
tan (A + B) = (tan A + tan B) / (1 - tan A tan B)
Cuando A = B, la fórmula anterior se convierte en
tan (A + A) = (tan A + tan A) / (1 - tan A tan A) =(2 tan A) / (1 - tan2A)
Así, la fórmula del ángulo doble de la función tan es
tan 2A = (2 tan A) / (1 - tan2A)