Cuál es el triángulo rectángulo

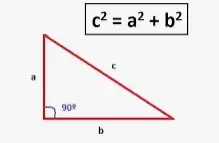
La definición de triángulo rectángulo dice que si uno de los ángulos de un triángulo es un ángulo recto - 90º, el triángulo se llama triángulo rectángulo o simplemente, triángulo rectángulo. En la imagen dada, el triángulo ABC es un triángulo rectángulo, donde tenemos la base, la altura y la hipotenusa. Aquí AB es la base, AC es la altura y BC es la hipotenusa. La hipotenusa es el lado importante de un triángulo rectángulo que es el más grande y está opuesto al ángulo recto dentro del triángulo.

Triángulo rectángulo

Aquí podemos haber comprendido las distintas características de un triángulo rectángulo. Las características del triángulo ABC son las siguientes:

• AC es la altura, altitud o perpendicular
• AB es la base
• AC ⊥ AB
• ∠A=90º

El lado BC opuesto al ángulo recto se llama hipotenusa y es el lado más largo del triángulo rectángulo.

Algunos ejemplos de triángulos rectángulos en nuestra vida cotidiana son la rebanada de pan triangular, un trozo de papel cuadrado doblado en diagonal o la escala triangular 30-60-90 de una caja de geometría.

Fórmula del triángulo rectángulo

El gran filósofo griego Pitágoras derivó una importante fórmula para un triángulo rectángulo. La fórmula establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos catetos. En su honor recibió el nombre de teorema de Pitágoras. La fórmula del triángulo rectángulo se puede representar de la siguiente manera: El cuadrado de la hipotenusa es igual a la suma del cuadrado de la base y el cuadrado de la altura.

En un triángulo rectángulo tenemos: (Hipotenusa)2 = (Base)2 + (Altitud)2

Triplete pitagórico: Los tres números que satisfacen la ecuación anterior son los tripletes pitagóricos. Por ejemplo, (3, 4, 5) es un triplete pitagórico porque sabemos que 32= 9, 42 = 16, y 52 = 25 y, 9 +16 = 25. Por lo tanto, 32 + 42 = 52 Estos tres números que cumplen esta condición se denominan triplete pitagórico. Otros ejemplos de triples pitagóricos son (6, 8, 10) y (12, 5, 13).

Tipos de triángulos rectángulos

Hemos aprendido que uno de los ángulos de un triángulo rectángulo es de 90º. Esto implica que los otros dos ángulos del triángulo serán ángulos agudos. Existen algunos triángulos rectángulos especiales: los triángulos rectángulos isósceles y los triángulos rectángulos escalenos. El triángulo que tiene los otros dos ángulos iguales se denomina triángulo rectángulo isósceles y el que tiene los otros dos ángulos con valores diferentes se llama triángulo rectángulo escaleno.

Triángulo rectángulo isósceles

Un triángulo rectángulo isósceles se denomina triángulo 90º-45º- 45º. En el triángulo ABC, el ángulo A = 90º; por tanto, según la definición de triángulo rectángulo, el triángulo ABC es un triángulo rectángulo. También AB = AC; como los dos lados son iguales, el triángulo es también un triángulo isósceles. Como AB = AC, los ángulos de la base son iguales. Sabemos que la suma de los ángulos de un triángulo es 180º. Por lo tanto, los ángulos de la base suman 90º, lo que implica que son de 45º cada uno. Así que en un triángulo rectángulo isósceles, los ángulos serán siempre 90º-45º- 45º.

Triángulo rectángulo escaleno

Un triángulo rectángulo escaleno es un triángulo en el que uno de los ángulos es de 90º y los otros dos ángulos que llegan hasta 90º son de distinta medida. En el triángulo PQR, ∠Q =90º, por tanto, es un triángulo rectángulo. PQ no es igual a QR, por lo que es un triángulo escaleno. También hay un caso especial de triángulo escaleno 30º-60º-90º que también es un triángulo rectángulo en el que la relación entre el lado más largo del triángulo y su lado más corto es 2:1. El lado opuesto al ángulo de 30º es el lado más corto.

Vídeos de Cuál es el triángulo rectángulo