Curtosis estadística

Esta pesadez o ligereza en las colas suele significar que sus datos parecen más planos (o menos planos) en comparación con la distribución normal. La distribución normal estándar tiene una curtosis de 3, por lo que si sus valores se acercan a esa cifra, las colas de su gráfico son casi normales. Estas distribuciones se denominan mesocúrticas.

La kurtosis proporciona información sobre el grado de inclinación de una distribución de datos. El pico de una distribución de datos es el grado de concentración de los valores de los datos en torno a la media. Los conjuntos de datos con una curtosis alta tienden a tener un pico claro cerca de la media y tienden a disminuir rápidamente, y tienen colas pesadas. Los conjuntos de datos con una curtosis baja tienden a tener una cima plana cerca de la media en lugar de un pico pronunciado.

Las distribuciones de datos que tienen las mismas medias, las mismas desviaciones estándar y los mismos grados de asimetría pueden tener diferentes curtosis porque pueden tener diferentes grados de pico.

Mesocúrtica

Las distribuciones mesocurticas se definen técnicamente por tener una curtosis de cero, aunque la distribución no tiene que ser exactamente cero para que se clasifique como mesocurtica. Las distribuciones mesocurticas más comunes son:

• La distribución normal.
• Cualquier distribución con forma gaussiana (normal) y probabilidad cero en otros lugares de la recta real.
• La distribución binomial es mesocúrtica para algunos valores (por ejemplo, para p = 1/2±√(1/12).

¿Qué es el exceso de curtosis?

El exceso de curtosis suele definirse como kurt - 3 (véase la nota importante sobre las ecuaciones). Es una medida de cómo las colas de la distribución se comparan con la normal (Aldrich, E, 2014).

• El exceso de kurt para la distribución normal es 0 (es decir, 3 -3 = 0).
• El exceso negativo equivale a colas más ligeras que la distribución normal.
• Un exceso positivo equivale a colas más pesadas que la normal.

Cálculo de la curtosis

El grado de inclinación de una distribución se mide por la curtosis. Nos indica hasta qué punto la distribución es más o menos atípica (con más o menos cola) que la distribución normal.

Es difícil discernir los diferentes tipos de curtosis a partir de los gráficos de densidad (panel de la izquierda) porque las colas son cercanas a cero en todas las distribuciones. Pero las diferencias en las colas son fáciles de ver en los gráficos de cuantiles normales (panel de la derecha).

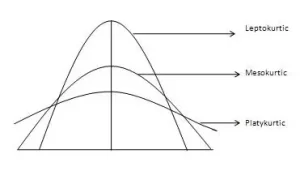
La curva normal se denomina curva mesocúrtica. Si la curva de una distribución es más propensa a los valores atípicos (o con colas más pesadas) que una curva normal o mesocúrtica, se denomina curva leptocúrtica. Si una curva es menos propensa a los valores atípicos (o con colas más ligeras) que una curva normal, se denomina curva platicúrtica.

Vídeos de Curtosis estadística