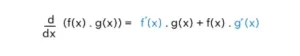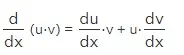Derivada multiplicación

La regla del producto en cálculo es un método utilizado para encontrar la derivada de cualquier función dada en forma de producto obtenido por la multiplicación de dos funciones diferenciables cualesquiera. La regla del producto en palabras dice que la derivada de un producto de dos funciones diferenciables es igual a la suma del producto de la segunda función con la diferenciación de la primera función y el producto de la primera función con la diferenciación de la segunda función. Eso significa que si nos dan una función de la forma: f(x)-g(x), podemos encontrar la derivada de esta función utilizando la derivada de la regla del producto como,

Fórmula de la regla del producto

Podemos calcular la derivada o evaluar la diferenciación del producto de dos funciones utilizando la fórmula de la regla del producto en Cálculo. La fórmula de la regla del producto es la siguiente

donde

f(x) = Producto de las funciones diferenciables u(x) y v(x)
u(x), v(x) = Funciones diferenciables
u'(x) = Derivada de la función u(x)
v'(x) = Derivada de la función v(x)

Derivación de la fórmula de la regla del producto

En la sección anterior, aprendimos sobre la fórmula del producto para encontrar las derivadas del producto de dos funciones diferenciables. Para dos funciones cualesquiera, la regla del producto puede darse en notación de Lagrange como

(u v)' = u'-v + u-v'

o en la notación de Leibniz como:

¿Cómo aplicar la regla del producto en la diferenciación?

Para encontrar la derivada de la función de la forma h(x) = f(x)g(x), tanto f(x) como g(x) deben ser funciones diferenciables. Podemos aplicar los siguientes pasos dados para encontrar la derivada de una función diferenciable h(x) = f(x)g(x) utilizando la regla del producto.

• Paso 1: Anota los valores de f(x) y g(x).
• Paso 2: Encuentra los valores de f'(x) y g'(x) y aplica la fórmula de la regla del producto, dada como: h'(x) = d/dx f(x)-g(x) = [g(x) × f'(x) + f(x) × g'(x)].

Vídeos de Derivada multiplicación