Fórmula del cuadrado

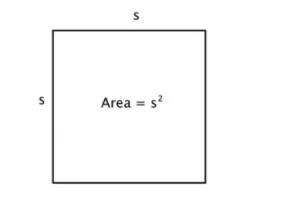
Todos conocemos la figura del cuadrado. Es un cuadrilátero en el que los cuatro lados y ángulos son iguales. Los cuatro ángulos tienen 90 grados cada uno, es decir, son ángulos rectos.

• Área de un cuadrado = a²
• El perímetro de un Cuadrado =4a
• Diagonal de un Cuadrado=a√2

Donde "a" es la longitud de un lado del cuadrado.

Propiedades de un cuadrado

• Las longitudes de los cuatro lados de un cuadrado son iguales.
• Las dos diagonales se bisecan en ángulo recto, es decir, 90º
• Las longitudes de las diagonales de un cuadrado son iguales.

Derivación de la fórmula del cuadrado

Para comprender mejor el concepto, veamos la derivación del área de un cuadrado. Consideremos un cuadrado en el que las longitudes de sus lados son "a" unidades y la diagonal es "d" unidades respectivamente. Como todos sabemos, el área de un cuadrado es la región que está encerrada dentro de su límite. Como ya hemos mencionado, un cuadrado es un caso especial de un rectángulo que tiene sus dos lados adyacentes de igual longitud. Por lo tanto, el área se puede expresar como

• Área de un rectángulo = Longitud × Anchura
• Área de un cuadrado = Longitud x Anchura
  Área de un cuadrado = a× a = a²

Derivación del perímetro de un cuadrado

El perímetro de un cuadrado es la longitud total de su frontera. El límite de un cuadrado está representado por la suma de la longitud de todos los lados. Por lo tanto, el perímetro se expresa como

• Perímetro de un cuadrado = longitud de 4 lados
  Perímetro de un cuadrado = a+ a + a + a = 4a

Derivación de la longitud de la diagonal de un cuadrado

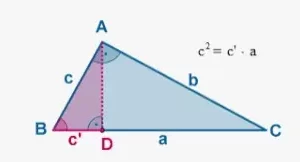
Como todos sabéis la diagonal es una línea que une los dos lados opuestos en un polígono. Por lo tanto, para calcular la longitud de la diagonal de un cuadrado, utilizamos el Teorema de Pitágoras. Si marcamos una diagonal en el cuadrado, nos daremos cuenta de que la diagonal divide el cuadrado en dos triángulos rectángulos. Ahora, los dos lados adyacentes de un cuadrado tienen la misma longitud. Y el triángulo rectángulo funciona como un triángulo isósceles con cada uno de sus lados de longitud 'a' unidades.

Así, podemos aplicar el teorema de Pitágoras sobre estos triángulos que tienen base y perpendicular de 'a' unidades e hipotenusa de 'b' unidades. Así, según la fórmula tenemos:

d²=a²+a²
d = √2 a²
d = a √2 unidades

Ejemplos resueltos

Ahora que ya hemos entendido un poco el concepto y el significado de la fórmula del cuadrado, vamos a probar algunos ejemplos para profundizar en el tema

- El lado de un cuadrado es de 5 metros. ¿Cuál es el área del cuadrado en m2?

Solución - Como sabemos, los lados de un cuadrado son de igual tamaño. Y la fórmula del área del cuadrado es a × a donde a es el lado del cuadrado. Por lo tanto

Área = 5m × 5m = 25 m²

- El perímetro de un cuadrado es de 24 cm. ¿Cuál es el área del cuadrado es cm2

Solución - El perímetro de un cuadrado es 4 × a, donde a es el lado del cuadrado

4 × a =24
a = 24 ÷ 4 = 6
Área = a × a = 6 cm × 6 cm = 36 cm2

- El lado de un cuadrado es de 5 cm. Si se duplica su lado, ¿cuántas veces es mayor el área del nuevo cuadrado que la del anterior?

Solución - El área del primer cuadrado es 5 cm × 5 cm = 25 cms. La nueva longitud = 5 cm + 5 cm = 10 cm

El área del nuevo cuadrado es de 10 cm × 10 cm = 100 cm2. Por tanto, el área es 4 veces mayor.

Vídeos de Fórmula del cuadrado