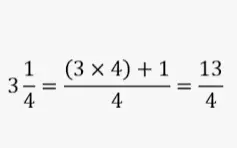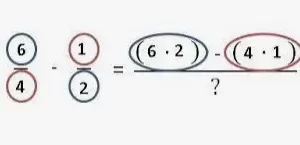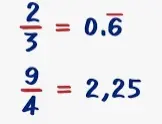Fracciones de división

Dividir fracciones es igual a la multiplicación de una fracción por el recíproco de otra fracción. Una fracción tiene un numerador y un denominador. Cuando dividimos una fracción por otra, entonces casi multiplicamos las fracciones con un giro.

Los pasos involucrados en la división de fracciones son

• Encontrar el recíproco
• Conversión de la división en multiplicación
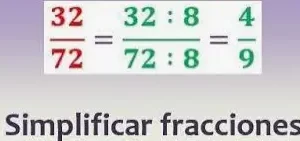
• Simplificación

Supongamos que ½ se divide por ⅔. El recíproco de ⅔ es 3/2. Ahora, ½ se multiplica por 3/2 para obtener el valor de la división requerido.

¿Qué son las fracciones?

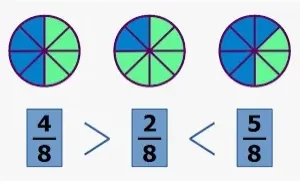
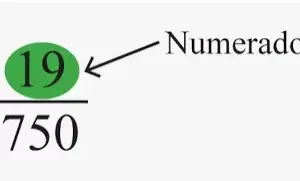
Una fracción es una parte de un valor o número entero. Se representa por p/q o a/b o m/n, etc. La parte superior de una fracción se llama numerador y la parte inferior es el denominador. Ejemplos de fracciones son ½, ¼, ⅔, ⅗, etc.

Todas las operaciones aritméticas como la suma, la resta, la multiplicación y la división se pueden realizar con las fracciones. Aprendamos aquí a dividir una fracción por una fracción, por un número entero y por un número mixto con la ayuda de ejemplos, con pasos sencillos.

¿Qué significa dividir fracciones?

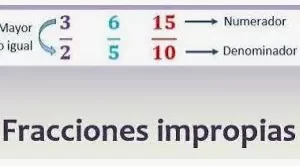
Dividir fracciones no es más que multiplicar las fracciones invirtiendo uno de los dos números de la fracción o escribiendo el recíproco de una de las fracciones. Por recíproco se entiende que si una fracción se da como a/b, entonces el recíproco de la misma será b/a. Así, intercambiando la posición del numerador y del denominador entre sí

a/b ÷ c/d = a/b × d/c

¿Cómo se dividen las fracciones?

La división de fracciones se puede clasificar en tres formas diferentes. Son las siguientes

• Dividiendo fracciones por una fracción
• Dividiendo fracciones por un número entero
• Dividiendo fracciones por una fracción mixta

Dividir una fracción por una fracción

En tres sencillos pasos, podemos resolver la división de fracciones convirtiéndolas en la multiplicación de fracciones. Aprendamos uno por uno.

Paso 1: Escribir el recíproco del segundo número de la fracción y multiplicarlo por el primer número de la fracción

Paso 2: Multiplicar los numeradores y denominadores de ambas fracciones

Paso 3: Simplificar el número de la fracción

En general, si a/b es una fracción que se divide por c/d. Entonces podemos resolver la división como

a/b ÷ c/d = a/b × d/c
a/b ÷ c/d = a×d / b×c
a/b ÷ c/d = ad/bc

Puedes ver en las expresiones anteriores. El a/b se divide por c/d, entonces podemos escribirlo como a/b multiplicado por d/c (recíproco de c/d). Y en el siguiente paso, tenemos que multiplicar tanto el numerador a & d como el denominador, c & d. Por lo tanto, podemos simplificar el resto del cálculo.

Vídeos de Fracciones de división