Funciones exponenciales

Las funciones exponenciales son ejemplos de funciones no algebraicas o trascendentales, es decir, funciones que no pueden representarse como el producto, la suma y la diferencia de variables elevadas a alguna potencia entera no negativa. Otras funciones trascendentales comunes son las funciones logarítmicas y las funciones trigonométricas. Las funciones exponenciales surgen con frecuencia y describen cuantitativamente una serie de fenómenos de la física, como la desintegración radiactiva, en la que la tasa de cambio de un proceso o sustancia depende directamente de su valor actual.

Función exponencial

La función exponencial es un tipo de función matemática que sirve para encontrar el crecimiento o la decadencia de la población, el dinero, el precio, etc. que crecen o decaen exponencialmente. Jonathan estaba leyendo un artículo sobre las últimas investigaciones realizadas sobre el crecimiento bacteriano. Leyó que se había realizado un experimento con una bacteria. Después de la primera hora, la bacteria se duplicó y llegó a ser dos. Después de la segunda hora, el número era de cuatro. A cada hora el número de bacterias aumentaba. Pensó en cuál sería el número de bacterias después de 100 horas si este patrón continúa. Cuando le preguntó a su profesor sobre el mismo, la respuesta que obtuvo fue el concepto de función exponencial.

¿Qué es la función exponencial?

La función exponencial, como su nombre indica, implica exponentes. Pero ten en cuenta que una función exponencial tiene una constante como base y una variable como exponente, pero no al revés (si una función tiene una variable como base y una constante como exponente, entonces es una función de potencia, pero no una función exponencial). Una función exponencial puede tener una de las siguientes formas.

Definición de función exponencial

En matemáticas, una función exponencial es una función de la forma f (x) = ax, donde "x" es una variable y "a" es una constante que se llama la base de la función y debe ser mayor que 0.

Ejemplos de la función exponencial

Estos son algunos ejemplos de función exponencial.

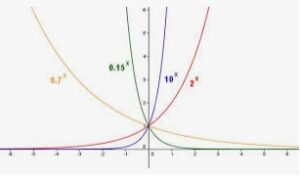
f(x) = 2x
f(x) = (1/2)x
f(x) = 3e2x
f(x) = 4 (3)-0.5x

Fórmula de la función exponencial

Una función exponencial básica, desde su definición, es de la forma f(x) = bx, donde 'b' es una constante y 'x' es una variable. Una de las funciones exponenciales más populares es f(x) = ex, donde 'e' es el "número de Euler" y e = 2,718..... Si ampliamos las posibilidades de las distintas funciones exponenciales, una función exponencial puede implicar una constante como múltiplo de la variable en su potencia, es decir, una función exponencial también puede ser de la forma f(x) = ekx. Además, también puede ser de la forma f(x) = p ekx, donde "p" es una constante. Así, una función exponencial puede tener una de las siguientes formas

• f(x) = bx
• f(x) = abx
• f(x) = abcx
• f(x) = ex
• f(x) = ekx
• f(x) = p ekx

Aquí, aparte de "x", todas las demás letras son constantes, "x" es una variable, y f(x) es una función exponencial en términos de x. Además, ten en cuenta que la base de cada función exponencial debe ser un número positivo, es decir, en las funciones anteriores, b > 0 y e > 0. Además, b no debe ser igual a 1 (si b = 1, la función f(x) = bx se convierte en f(x) = 1 y, en este caso, la función es lineal pero NO exponencial).

La función exponencial surge siempre que el valor de una cantidad aumenta en el crecimiento exponencial y disminuye en el decaimiento exponencial.

Reglas de la función exponencial

Las reglas de la función exponencial son las mismas que las de los exponentes. Estas son algunas reglas de los exponentes.

• Ley del exponente cero: a0 = 1
• Ley del producto: am × an = am+n
• Ley del cociente: am/an = am-n
• Ley de la potencia de una potencia: (am)n = amn
• Ley de la potencia de un producto: (ab)m = ambm
• Ley de la potencia de un cociente: (a/b)m = am/bm
• Ley del Exponente Negativo: a-m = 1/am

Vídeos de Funciones exponenciales