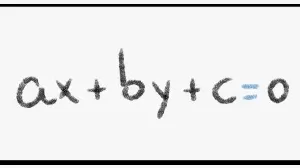Poliedros irregulares

Una forma sólida delimitada por polígonos se llama poliedro. La palabra poliédrica es el plural de la palabra poliedro.

• Caras: Los polígonos que forman un poliedro se conocen como sus caras.
• Aristas: Los segmentos de línea comunes a las caras que se cruzan en un poliedro se conocen como aristas.
• Vértices: Los puntos de intersección de las aristas de un poliedro se denominan vértices.

Base de la definición

Cualquier poliedro puede construirse a partir de diferentes tipos de elementos o entidades, cada uno de ellos asociado a un número diferente de dimensiones:

• 3 dimensiones: El cuerpo está delimitado por las caras, y suele ser el volumen encerrado por ellas.
• 2 dimensiones: Una cara es un polígono delimitado por un circuito de aristas, y que suele incluir la región plana (plana) dentro del límite. El conjunto de estas caras poligonales constituye la superficie poliédrica.
• 1 dimensión: Una arista une un vértice con otro y una cara con otra, y suele ser un segmento de línea. El conjunto de aristas constituye el esqueleto poliédrico.
• 0 dimensiones: Un vértice (vértices plurales) es un punto de esquina.
• -1 dimensión: La nulidad es una especie de no entidad requerida por las teorías abstractas.

En general, en matemáticas y otras disciplinas, "poliedro" se utiliza para referirse a una variedad de construcciones relacionadas, algunas geométricas y otras puramente algebraicas o abstractas.

Una característica que define a casi todos los tipos de poliedros es que sólo dos caras se unen a lo largo de cualquier arista común. Esto garantiza que la superficie poliédrica esté conectada de forma continua y no termine de forma abrupta o se divida en diferentes direcciones.

Un poliedro es un ejemplo tridimensional del politopo más general en cualquier número de dimensiones.

Características

Los poliedros suelen denominarse en función del número de caras. El sistema de nomenclatura se basa de nuevo en el griego clásico, por ejemplo, tetraedro (4), pentaedro (5), hexaedro (6), heptaedro (7), triacontaedro (30), etc.

A menudo esto se califica con una descripción de los tipos de caras presentes, por ejemplo el dodecaedro rómbico frente al dodecaedro pentagonal.

Otros nombres comunes indican que se ha realizado alguna operación en un poliedro más simple, por ejemplo el cubo truncado parece un cubo con las esquinas cortadas, y tiene 14 caras (por lo que también es un ejemplo de tetrakaidecaedro).

Algunos poliedros especiales han recibido sus propios nombres a lo largo de los años, como el monstruo de Miller o el poliedro de Szilassi.

Aristas

Las aristas tienen dos características importantes (a menos que el poliedro sea complejo):

• Una arista une sólo dos vértices.
• Una arista une sólo dos caras.
• Estas dos características son duales entre sí.

Característica de Euler

La característica de Euler χ relaciona el número de vértices V, aristas E y caras F de un poliedro:

χ = V - E + F

Para un poliedro simplemente conectado, χ = 2.

Dualidad

Para cada poliedro existe un poliedro dual que tiene caras en lugar de los vértices del original y viceversa. En la mayoría de los casos, el dual se puede obtener mediante el proceso de reciprocidad esférica.

Figura de los vértices

Para cada vértice se puede definir una figura de vértice formada por los vértices unidos a él. Se dice que el vértice es regular si éste es un polígono regular y simétrico respecto al poliedro completo.

Vídeos de Poliedros irregulares