Semejanza de triángulos
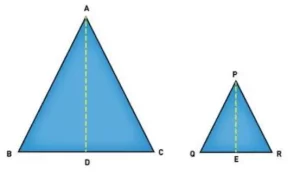
Dos triángulos son semejantes si tienen la misma proporción de lados correspondientes e igual par de ángulos correspondientes.
Si dos o más figuras tienen la misma forma, pero sus tamaños son diferentes, estos objetos se llaman figuras semejantes. Consideremos un aro de hula y la rueda de una bicicleta, las formas de estos dos objetos son similares entre sí ya que sus formas son iguales.
Figuras similares
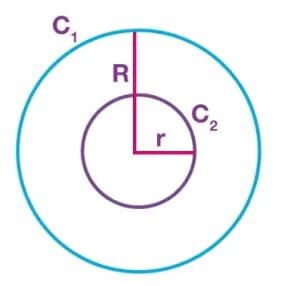
En la figura anterior, dos círculos C1 y C2 de radio R y r respectivamente son semejantes porque tienen la misma forma, pero no necesariamente el mismo tamaño. Por tanto, podemos decir que C1~ C2.
Hay que tener en cuenta que dos circunferencias siempre tienen la misma forma, independientemente de su diámetro. Por lo tanto, dos círculos son siempre similares.
El triángulo es el polígono de tres lados. La condición para la similitud de los triángulos es;
i) Los ángulos correspondientes de ambos triángulos son iguales, y
ii) Los lados correspondientes de ambos triángulos son proporcionales entre sí.
Ejemplo de triángulo semejante
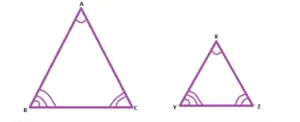
En la figura dada, dos triángulos ΔABC y ΔXYZ son semejantes sólo si,
i) ∠A = ∠X, ∠B = ∠Y y ∠C = ∠Z
ii) AB/XY = BC/YZ = AC/XZ (Proporciones de triángulos semejantes).
Por lo tanto, si se cumplen las condiciones mencionadas, entonces podemos decir que ΔABC ~ ΔXYZ
Es interesante saber que si los ángulos correspondientes de dos triángulos son iguales, entonces tales triángulos se conocen como triángulos equiangulares. Para dos triángulos equiangulares podemos enunciar el Teorema Básico de la Proporcionalidad (más conocido como Teorema de Tales) de la siguiente manera:
Para dos triángulos equiangulares, la relación de dos lados cualesquiera es siempre la misma.
Propiedades
- Ambos tienen la misma forma pero los tamaños pueden ser diferentes
- Cada par de ángulos correspondientes son iguales
- La relación de los lados correspondientes es la misma
Fórmulas
Según la definición, dos triángulos son semejantes si sus ángulos correspondientes son congruentes y sus lados correspondientes son proporcionales. Por lo tanto, podemos encontrar las dimensiones de un triángulo con la ayuda de otro triángulo. Si ABC y XYZ son dos triángulos semejantes, con la ayuda de las fórmulas dadas a continuación, podemos encontrar los ángulos y las longitudes de los lados correspondientes.
∠A = ∠X, ∠B = ∠Y y ∠C = ∠Z
AB/XY = BC/YZ = AC/XZ
Una vez conocidas todas las dimensiones y ángulos de los triángulos, es fácil encontrar el área de los triángulos semejantes.
Vídeos de Semejanza de triángulos
Entradas Relacionadas
Contenido