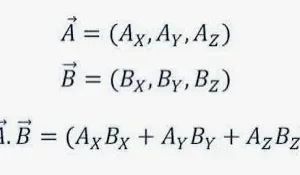¿Qué es una componente?

En situaciones en las que los vectores se dirigen en ángulos a los ejes de coordenadas habituales, se empleará un truco matemático útil para transformar el vector en dos partes con cada parte dirigida a lo largo de los ejes de coordenadas. Por ejemplo, un vector dirigido hacia el noroeste puede considerarse que tiene dos partes: una hacia el norte y otra hacia el oeste. Un vector dirigido hacia arriba y hacia la derecha puede considerarse que tiene dos partes: una hacia arriba y otra hacia la derecha.

Componente de un vector

Las componentes de un vector dan una división del vector. El vector se divide con referencia a cada uno de los ejes, y podemos calcular las componentes de un vector. Los componentes individuales de un vector pueden combinarse posteriormente para obtener la representación vectorial completa. Los vectores se representan generalmente en un plano de coordenadas bidimensional, con un eje x, un eje y, o en un espacio tridimensional, que contiene el eje x, el eje y y el eje z, respectivamente. Los vectores son representaciones matemáticas generales con dirección y magnitud.

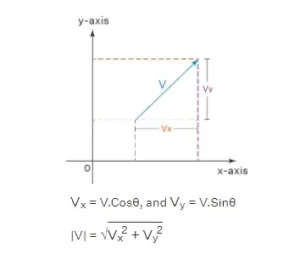
En un sistema de coordenadas bidimensional, la dirección del vector es el ángulo que forma el vector con el eje x positivo. Sea V el vector y θ el ángulo que forma el vector con el eje x positivo. Además, tenemos las componentes de este vector a lo largo del eje x y y como Vx, y Vy respectivamente. Estos componentes se pueden calcular mediante las siguientes expresiones.

Además, los vectores también se representan como en el espacio tridimensional. Aquí i,j y k son los vectores unitarios a lo largo del eje x, eje y y eje z respectivamente. Estos vectores unitarios ayudan a identificar las componentes de los vectores con referencia a cada uno de los ejes. Las componentes del vector A con respecto al eje x, eje y, eje z, son a, b, c respectivamente.

Ejemplo de componentes de un vector

Encuentra las componentes x e y de un vector que tiene una magnitud de 12 y forma un ángulo de 45 grados con el eje x positivo.

Solución:

El vector dado es V= 12, y forma un ángulo θ = 45º.

La componente x del vector = V x = VCosθ = 12.Cos45º = 12.(1/√2) = 6√2.

La componente y del vector = V y = VSinθ = 12.Sin45º = 12.(1/√2) = 6√2.

Por tanto, la componente x y la componente y del vector son ambas iguales a 6√2.

Vídeos de Componente de un vector