Método de máxima verosimilitud

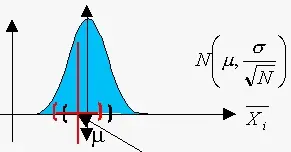
La MLE toma distribuciones de probabilidad conocidas (como la distribución normal) y compara conjuntos de datos con esas distribuciones para encontrar una correspondencia adecuada para los datos. Una familia de distribuciones puede tener una cantidad infinita de parámetros posibles. Por ejemplo, la media de la distribución normal podría ser igual a cero, o podría ser igual a diez mil millones y más. La estimación de máxima verosimilitud es una forma de encontrar los parámetros de la población que más probablemente haya generado la muestra que se está analizando. El grado de coincidencia de los datos con el modelo se conoce como "bondad de ajuste".

Por ejemplo, un investigador puede estar interesado en averiguar el aumento de peso medio de las ratas que consumen una determinada dieta. El investigador no puede pesar a todas las ratas de la población, por lo que toma una muestra. El aumento de peso de las ratas tiende a seguir una distribución normal; la estimación de máxima verosimilitud puede utilizarse para encontrar la media y la varianza del aumento de peso en la población general basándose en esta muestra.

La estimación de máxima verosimilitud elige los parámetros del modelo basándose en los valores que maximizan la función de verosimilitud.

La función de verosimilitud

La probabilidad de una muestra es la probabilidad de obtener esa muestra, dado un modelo de distribución de probabilidad especificado. La función de verosimilitud es una forma de expresar esa probabilidad: los parámetros que maximizan la probabilidad de obtener esa muestra son los estimadores de máxima verosimilitud.

Supongamos que se tiene un conjunto de variables aleatorias X1, X2...Xn tomadas de una distribución poblacional desconocida con parámetro Θ. Esta distribución tiene una función de densidad de probabilidad (PDF) de f(Xi,Θ) donde f es el modelo, Xi es el conjunto de variables aleatorias y Θ es el parámetro desconocido. Para la función de máxima verosimilitud se quiere saber cuál es el valor más probable de Θ, dado el conjunto de variables aleatorias Xi. La función de densidad de probabilidad conjunta para este ejemplo es:

Vídeos de Método de máxima verosimilitud