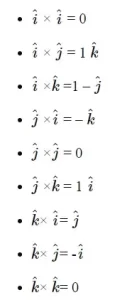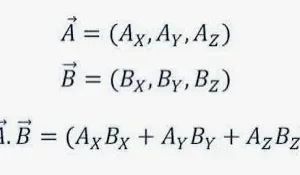Propiedades del producto vectorial

El producto vectorial también significa que es el producto cruzado de dos vectores.

Si tenemos dos vectores a y b, el producto vectorial de a y b es c.

c = a × b

Así que este a × b en realidad significa que la magnitud de c = ab sinθ donde θ es el ángulo entre a y b y la dirección de c es perpendicular tanto a a como a b. Ahora, ¿cuál debería ser la dirección de este producto cruzado? Para averiguar la dirección, utilizamos la regla que llamamos "regla del pulgar derecho".

Supongamos que queremos averiguar la dirección de a × b, para lo cual doblamos los dedos desde la dirección de a hasta la de b. Así, si doblamos los dedos en una dirección como la que se muestra en la figura anterior, el pulgar apunta en la dirección de c, es decir, en dirección ascendente. Este pulgar denota la dirección del producto cruzado.

Al aplicar las reglas de dirección, la rotación debe llevarse a ángulos más pequeños que es <180° entre a y b. Así que los dedos deben estar siempre curvados en ángulo agudo entre a y b.

Propiedades del producto cruzado vectorial

1] El producto vectorial no es conmutativo. Esto significa que a × b ≠ b × a

Hemos visto que a × b = c aquí el pulgar apunta hacia arriba. Mientras que en b × a el pulgar apuntará en dirección hacia abajo. Por lo tanto, b × a = - c. Así que no es conmutativo.

2] No hay ningún cambio en la reflexión.

¿Qué le ocurre a a × b en la reflexión? Supongamos que el vector a va y choca con el espejo, por lo que la dirección de a se convertirá en - a. Así que en la reflexión, a se convertirá en - a y b en - b. Ahora a × b se convertirá en -a × -b = a × b

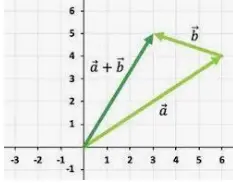
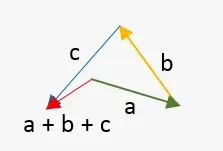
3] Es distributiva con respecto a la suma de vectores.

Esto significa que si a × ( b + c ) = a × b + a × c. Esto es cierto en el caso de la adición.

Producto vectorial de vectores unitarios

Vídeos de Propiedades del producto vectorial