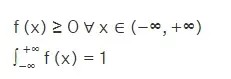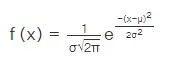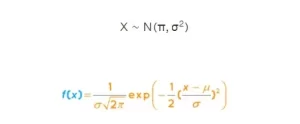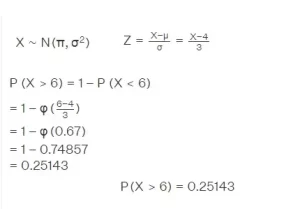Distribución normal fórmula

La distribución normal se define por la función de densidad de probabilidad f(x) para la variable aleatoria continua X considerada en el sistema. Es una función cuya integral a través de un intervalo (digamos de x a x + dx) da la probabilidad de la variable aleatoria X, considerando los valores entre x y x + dx. Como habrá infinitos valores entre x y x + dx, se considera un intervalo de x, y se define una función de densidad de probabilidad continua como

Para una distribución normal de una variable aleatoria X con la media = μ y la varianza = σ2, la densidad de probabilidad f(x) viene dada por:

Una representación equivalente:

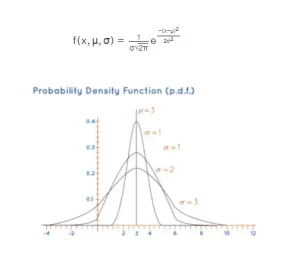
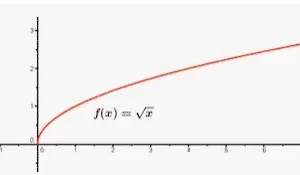
Para una μ = 3 y una σ que va de 1 a 3, la función de densidad de probabilidad (f.d.p.) es como:

La función de densidad de probabilidad de la distribución normal o gaussiana viene dada por;

Donde, x es la variable μ es la media σ es la desviación estándar

Ejemplo con la fórmula de la distribución normal

Ejemplo 1: Si X∼ N ( 4 , 9 ) , encontrar P ( X > 6 ) utilizando la fórmula de la distribución normal.

Solución:

Cuando una variable X sigue una distribución normal, con media μ y varianza σ2, se denota por:

Vídeos de Distribución normal fórmula