Función convexa

Una forma convexa es lo contrario de una forma cóncava. Se curva hacia fuera y su centro es más grueso que sus bordes. Si coges un balón de fútbol o de rugby y lo colocas como si fueras a patearlo, verás que tiene una forma convexa: sus extremos son puntiagudos y tiene un centro grueso.

Al igual que cóncavo, convexo puede utilizarse como sustantivo para una superficie o línea que se curva hacia fuera, y también tiene un uso en geometría, donde describe un polígono con ángulos interiores menores o iguales a 180°.

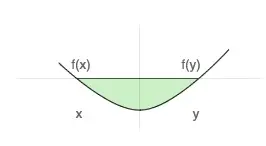
Geométricamente, una función es convexa si un segmento de línea trazado desde cualquier punto (x, f(x)) a otro punto (y, f(y)) -llamado cuerda de x a y- se encuentra en o por encima de la gráfica de f, como en la imagen siguiente:

Algebraicamente, f es convexa si, para cualquier x e y, y cualquier t entre 0 y 1, f( tx + (1-t)y ) <= t f(x) + (1-t) f(y). Una función es cóncava si -f es convexa, es decir, si la cuerda de x a y se encuentra en la gráfica de f o por debajo de ella. Es fácil ver que toda función lineal, cuya gráfica es una línea recta, es a la vez convexa y cóncava.

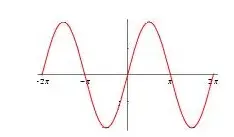
Una función no convexa "se curva hacia arriba y hacia abajo", no es ni convexa ni cóncava. Un ejemplo conocido es la función seno:

pero observe que esta función es convexa de -pi a 0, y cóncava de 0 a +pi. Si los límites de las variables restringen el dominio del objetivo y las restricciones a una región en la que las funciones son convexas, entonces el problema global es convexo.

Polígono convexo

Un polígono convexo es una figura cerrada en la que todos sus ángulos interiores son menores de 180° y los vértices apuntan hacia fuera. El término convexo se utiliza para referirse a una forma que tiene una curva o una superficie saliente. En otras palabras, todas las líneas del contorno son rectas y apuntan hacia fuera. Ejemplos del mundo real de polígonos convexos son un cartel, un balón de fútbol, un plato circular y muchos más. En geometría, hay muchas formas que pueden clasificarse como polígonos convexos. Por ejemplo, un hexágono es un polígono cerrado de seis lados. Dado que un hexágono tiene todos sus ángulos interiores menores de 180°, puede denominarse polígono convexo.

Vídeos de Función convexa