Aceleración centrípeta fórmula
¿Los tiovivos son un ejemplo perfecto de la forma en que se utiliza la fuerza para preservar un elemento de transferencia en un camino redondo. Su marco deseaba volar fuera del carrusel en una línea instantánea, sin embargo, sus dedos ejercieron una fuerza opuesta para mantenerlo. La tendencia de su marco para volar fuera de la merry-go-spherical se conoce como fuerza centrífuga. No es una fuerza real, pero sí una evidente. La fuerza que se utiliza junto con los dedos para vivir en el viaje es real, y es mucho conocido como la fuerza centrípeta. Vamos a investigar más sobre ella.
La aceleración centrípeta es la llamada aceleración a la vez en dirección al centro del círculo en un movimiento circular. Esto se describe a través de:
a = v2 / r
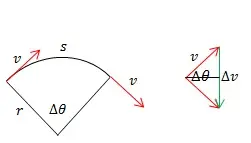
Donde v es la velocidad del elemento dentro de la línea tangencial al círculo, y r es el radio del círculo en el que se traslada. Piensa aproximadamente en lo que podría aparecer en caso de que hayas estado balanceando una pelota relacionada con una cuerda en un círculo, sin embargo, la cuerda se rompió. La pelota podría volar en una línea instantánea de su papel en el círculo en el momento en que la cuerda se rompió, y esto le ofrece un concepto de lo que v enfoque con dentro de la ecuación anterior.
Debido a que la 2ª ley de Newton establece que la fuerza = masa × aceleración, y tenemos una ecuación para la aceleración anterior, la fuerza centrípeta debe ser
F = m v2 / r
En esta ecuación, m se refiere a una masa.
Por lo tanto, para localizar la fuerza centrípeta, debes reconocer la masa del objeto, el radio del círculo en el que se desplaza y su velocidad tangencial. Utiliza la ecuación anterior para localizar la fuerza basándote totalmente en esos factores. Eleva al cuadrado la velocidad, multiplícala por la masa y luego divide el resultado por el radio del círculo.
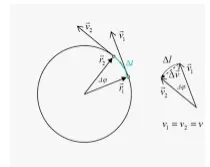
Un cuerpo que se mueve en un movimiento circular (de radio r) a velocidad constante (v) siempre está siendo acelerado. La aceleración es perpendicular a la dirección del movimiento (hacia el centro del círculo) y de magnitud v2 / r.
La dirección de la aceleración se deduce mediante argumentos de simetría. Si la aceleración apuntara fuera del plano del círculo, entonces el cuerpo saldría del plano del círculo; no lo hace, así que no lo hace. Si la aceleración apuntara en cualquier dirección que no fuera la perpendicular (izquierda o derecha), entonces el cuerpo se aceleraría o frenaría. No lo hace.
Vídeos de Aceleración centrípeta fórmula
Entradas Relacionadas
Contenido