Analisis

Cuál es el dominio de una función

Cual es el dominio de una funcion
Las funciones en matemáticas pueden compararse con las operaciones de una máquina expendedora (de refrescos). Cuando se introduce una determinada cantidad de dinero, se pueden seleccionar diferentes tipos de refrescos. Del mismo modo, en el caso de las funciones, introducimos diferentes números y obtenemos nuevos números como resultado. El dominio y el rango son los principales aspectos de las funciones. Puedes utilizar monedas de 25 centavos y billetes de un dólar para comprar un refresco. La máquina no te dará ningún sabor de refresco si introduces monedas de un céntimo. Por lo tanto, el dominio representa las entradas que podemos tener aquí, es decir, monedas de 25 centavos y billetes de un dólar. No importa la cantidad que pagues, no obtendrás una hamburguesa con queso de una máquina de refrescos. Por lo tanto, el rango son las posibles salidas que podemos tener aquí, es decir, los sabores de refresco en la máquina.

Cuál es el dominio de una función

El dominio y el rango se definen para una relación y son los conjuntos de todas las coordenadas x y todas las coordenadas y de los pares ordenados respectivamente. Por ejemplo, si la relación es, R = {(1, 2), (2, 2), (3, 3), (4, 3)}, entonces:

Dominio = el conjunto de todas las coordenadas x = {1, 2, 3, 4}
Rango = el conjunto de todas las coordenadas y = {2, 3}

Dominio y rango de una función

El dominio y el rango de una función son los componentes de una función. El dominio es el conjunto de todos los valores de entrada de una función y el rango es la posible salida dada por la función. Dominio→ Función → Rango. Si existe una función f: A →B tal que cada elemento de A es mapeado a elementos en B, entonces A es el dominio y B es el codominio. La imagen de un elemento 'a' bajo una relación R viene dada por 'b', donde (a,b) ∈ R. El rango de la función es el conjunto de imágenes. El dominio y el rango de una función se denotan en general como sigue: Dominio(f) = {x ∈ R} y rango(f)={f(x) : x ∈ dominio(f)}

Leer  Recorrido de una función

El dominio y rango de esta función f(x) = 2x viene dado por el dominio D ={x ∈ N } , rango R = {(y): y = 2x}

Dominio de una función

El dominio de una función se refiere a "todos los valores" que entran en una función. El dominio de una función es el conjunto de todas las entradas posibles para la función. Considere este cuadro como una función f(x) = 2x . Introduciendo los valores x = {1,2,3,4,...}, el dominio es simplemente el conjunto de los números naturales y los valores de salida se llaman el rango. Pero en general, f(x) = 2x está definida para todos los valores reales de x y por lo tanto su dominio es el conjunto de todos los números reales que se denota por (-∞, ∞). Aquí están las fórmulas generales utilizadas para encontrar el dominio de diferentes tipos de funciones. Aquí, R es el conjunto de todos los números reales.

  • Dominio de cualquier función polinómica (lineal, cuadrática, cúbica, etc) es R.
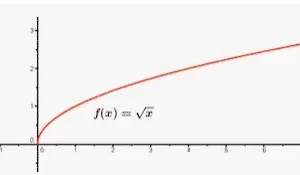
  • Dominio de una función raíz cuadrada √x es x≥0.
  • Dominio de una función exponencial es R.
  • Dominio de una función logarítmica es x>0.
  • Para hallar el dominio de una función racional y = f(x), pon el denominador ≠ 0.

Vídeos de cuál es el dominio de una función

Entradas Relacionadas

Límites al infinito
Diagrama de caja
Media fórmula

Contenido

Entradas Relacionadas