Función constante

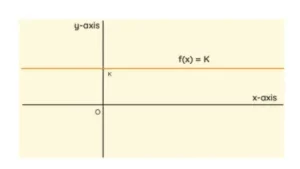
Una función constante es una función que tiene el mismo rango para diferentes valores del dominio. Gráficamente, una función constante es una línea recta paralela al eje x. El dominio de la función es el valor x y se representa en el eje x, y el rango de la función es y o f(x) que se marca con referencia al eje y.

Cualquier función puede considerarse como una función constante si es de la forma y = k, donde k es una constante y k es un número real cualquiera. También se escribe como f(x) = k. Hay que tener en cuenta que el valor de f(x) siempre será 'k', y es independiente del valor de x. En general, podemos definir una función constante como una función que siempre tiene el mismo valor constante, independientemente del valor de entrada.

Estos son algunos ejemplos de funciones constantes:

f(x) = 0
f(x) = 1
f(x) = π
f(x) = 3
f(x) =-0,3412454

f(x) es igual a cualquier otro número real que se te ocurra.

Una de las cosas interesantes de una función constante es que podemos introducir cualquier número real que queramos para x, y podemos saber instantáneamente el valor de la función en esa x sin usar ningún cálculo.

¿Cómo encontrar una función constante?

En esta sección, vamos a aprender a diferenciar entre una función constante y una función que no lo es. Para encontrar si una función es una función constante, haz lo siguiente:

Comprueba si es posible obtener diferentes salidas para diferentes entradas. Si esto es posible, entonces no es una función constante

Pero si sólo es posible obtener la misma salida independientemente de cuáles sean los valores de entrada, entonces es una función constante.

Consideremos la función y = x + 2. En este ejemplo, ¿podemos obtener distintas salidas variando los valores de entrada? La respuesta es sí, porque:

Si introducimos x = 1, obtenemos y = 1 + 2 o y = 3
Si introducimos x = 2, obtenemos y = 2 + 2 o y = 4.

Dado que obtenemos diferentes resultados al variar los valores de entrada, no se trata de una función constante.

Consideremos la función y = 3. Aquí, podemos notar que no importa cuál sea nuestro valor de x, o la entrada, es, y siempre será 3.

Si x = 3, y = 3 o si x = 5, y = 3

y es siempre 3 sin importar cuál sea nuestra entrada.

Dado que no podemos obtener diferentes salidas variando los valores de entrada, esta es una función constante.

Vídeos de Función constante