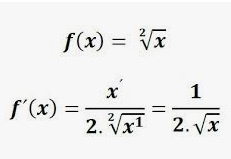Función radical
En matemáticas, el dominio de una función indica para qué valores de x es válida la función. Esto significa que cualquier valor dentro de ese dominio funcionará en la función, mientras que cualquier valor que caiga fuera del dominio no lo hará. Algunas funciones (como las funciones lineales) tienen dominios que incluyen todos los valores posibles de x. Otras (como las ecuaciones en las que x aparece dentro del denominador) excluyen ciertos valores de x para evitar la división por cero. Las funciones de raíz cuadrada tienen dominios más restringidos que algunas otras funciones, ya que el valor dentro de la raíz cuadrada (conocido como radicando) tiene que ser un número positivo para que el resultado sea "real".
El dominio de una función de raíz cuadrada son todos los valores de x que resultan en un radicando que es igual o mayor que cero.
Funciones de raíz cuadrada
Una función de raíz cuadrada es una función que contiene un radical, que es más comúnmente llamado raíz cuadrada. Si no estás seguro de cómo es esto
f(x) = \sqrt{x}f(x)= x
se considera una función de raíz cuadrada básica. En este caso, x no puede ser un número negativo; todos los radicales deben ser iguales o mayores que cero para que el resultado sea real. Si se pueden incluir números "imaginarios" (con i definida como la raíz cuadrada de -1), las cosas se complican más, pero en la mayoría de los casos sólo hay que considerar los números reales.
Esto no significa que todas las funciones de raíz cuadrada sean tan simples como la raíz cuadrada de un solo número. Las funciones de raíz cuadrada más complejas pueden tener cálculos dentro del radical, cálculos que modifican el resultado del radical o incluso un radical como parte de una función más grande (como la que aparece en el numerador o el denominador de una ecuación). Ejemplos de estas funciones más complejas son
f(x) = 2\sqrt{x + 3} \text{ o } g(x) = \sqrt{x - 4}f(x)=2
x+3
o
g(x)= x-4
Dominios de las funciones de raíz cuadrada
Para calcular el dominio de una función de raíz cuadrada, resuelve la desigualdad x ≥ 0 sustituyendo x por el radicando. Utilizando uno de los ejemplos anteriores, puedes encontrar el dominio de
f(x) = 2\sqrt{x + 3}f(x)=2
x+3
poniendo el radicando (x + 3) igual a x en la desigualdad. Esto le da la desigualdad de
x + 3 ≥ 0x+3≥0
que puedes resolver restando 3 por ambos lados. Esto te da una solución de x ≥ -3, lo que significa que tu dominio son todos los valores de x mayores o iguales a -3. También puedes escribir esto como [ -3, ∞), con el paréntesis de la izquierda mostrando que -3 es un límite específico, mientras que el paréntesis de la derecha muestra que ∞ no lo es. Como el radicando no puede ser negativo, sólo hay que calcular para valores positivos o cero.
