Cuerda matemáticas

Entre los demás segmentos de recta que se pueden trazar en una circunferencia, la cuerda es aquella cuyos puntos extremos se encuentran en la circunferencia. Observa la siguiente circunferencia para identificar la cuerda PQ. También se considera cuerda al diámetro que pasa por el centro de la circunferencia.

Propiedades de la cuerda de una circunferencia

A continuación se indican algunas propiedades importantes de las cuerdas de una circunferencia.

• La perpendicular a una cuerda, trazada desde el centro del círculo, biseca la cuerda.
• Las cuerdas de una circunferencia, equidistantes del centro de la circunferencia son iguales.
• Hay una y sólo una circunferencia que pasa por tres puntos colineales.
• Cuando se traza una cuerda del círculo, ésta divide el círculo en dos regiones, denominadas segmentos del círculo: el segmento mayor y el segmento menor.
• Una cuerda cuando se extiende infinitamente por ambos lados se convierte en una secante.

Fórmula de la cuerda del círculo

Existen dos fórmulas básicas para encontrar la longitud de la cuerda de una circunferencia:

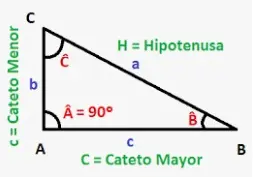
• Longitud de la cuerda utilizando la distancia perpendicular al centro = 2 × √(r2 - d2). Veamos la demostración y la derivación de esta fórmula. En la circunferencia dada a continuación, el radio 'r' es la hipotenusa del triángulo que se forma. La mediatriz 'd' es uno de los catetos del triángulo rectángulo. Sabemos que la mediatriz del centro de la circunferencia a la cuerda es la bisectriz de la cuerda. Por tanto, la mitad de la cuerda forma el otro cateto del triángulo rectángulo. Por el teorema de Pitágoras, (1/2 cuerda)2 + d2 = r2, lo que da además 1/2 de la longitud de la cuerda = √(r2 - d2). Por lo tanto, la longitud de la cuerda = 2 × √(r2 - d2)
• Longitud de la cuerda mediante trigonometría = 2 × r × sin(θ/2); donde "r" es el radio del círculo y "θ" es el ángulo subtendido en el centro por la cuerda.

Vídeos de Cuerda matemáticas