Tipos de poliedros
La palabra poliedro tiene varios significados imperceptibles en geometría y geometría algebraica. En geometría, un poliedro no es más que un sólido tridimensional formado por un grupo de polígonos, normalmente conectados por sus aristas. En otras palabras, un poliedro es una variante tridimensional del politopo más común, que define una dimensión arbitraria. El nombre plural de un poliedro es "poliedros" o, a veces, "poliedros".
El término "poliedro" se utiliza de forma algo diferente en topología algebraica. Aquí se define como un espacio construido a partir de "bloques de construcción" como segmentos de línea, triángulos, tetraedros y sus análogos de mayor dimensión, "fijándolos juntos" junto con sus caras. Un poliedro puede observarse como una intersección de semiespacios, mientras que un politopo es un poliedro acotado, como se muestra en la figura siguiente.
Los poliedros se clasifican en dos tipos en función de las aristas que tienen. Son:
- Poliedro regular
- Poliedro irregular
Entendamos estos tipos de polígonos junto con los ejemplos que aquí se presentan.
Poliedro regular
Un poliedro regular está formado por polígonos regulares, es decir, todas las aristas son congruentes. Estos sólidos también se llaman sólidos platónicos.
Ejemplos: Pirámide triangular y cubo
- Poliedro regular
- Poliedro irregular
Un poliedro irregular está formado por polígonos con formas diferentes en los que todos los elementos no son iguales. En este caso, todas las caras de un poliedro irregular no son congruentes.
Ejemplos: Prisma triangular y prisma octogonal
Poliedro irregular
Si se da el número de caras y el vértice de un poliedro, podemos encontrar las aristas mediante la fórmula del poliedro. Esta fórmula también se conoce como "fórmula de Euler".
F + V = E + 2
Aquí,
F = Número de caras del poliedro
V = Número de vértices del poliedro
E = Número de aristas del poliedro
Si conocemos dos de entre F, V y E, podemos encontrar el tercer valor.
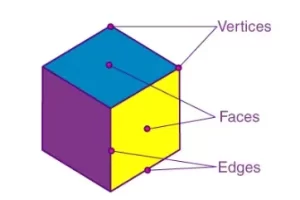
Todo poliedro tiene tres componentes significativos: caras, aristas y vértices.
- Caras: Las superficies planas que forman un poliedro se llaman caras. Estas caras son polígonos bidimensionales.
- Aristas: Los segmentos de línea formados por dos regiones o dos superficies planas (caras) se conocen como aristas.
- Vértices: El punto de intersección de las aristas se llama vértice del poliedro. Un poliedro puede tener varios vértices. También se conocen como vértices de un poliedro.
La siguiente figura muestra las caras, aristas y vértices de un hexaedro.
Caras, aristas y vértices del poliedro
Aquí,
El número de caras = 6
El número de aristas = 12
El número de vértices = 8
Verificación mediante la fórmula de Euler:
F = 6, E = 12, V = 8
F + V = E + 2
6 + 8 = 12 + 2
14 = 14
Forma de poliedro
Una forma tridimensional con caras poligonales planas, aristas rectas y esquinas o vértices agudos se llama poliedro. La palabra "poliedro" tiene su origen en dos palabras griegas: poly y hedron. Aquí, "poly" significa muchos y "hedron" indica superficie. Los nombres de los poliedros se definen por el número de caras que tiene.
Ejemplos de poliedros
Podemos observar (como se indica en la siguiente figura) varios poliedros en nuestra existencia diaria, como el cubo de Rubik, los dados, la bola Bucky, las pirámides, etc.
Vídeos de Tipos de poliedros
Entradas Relacionadas
Contenido