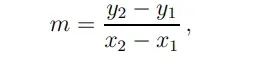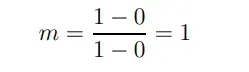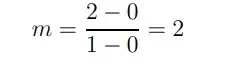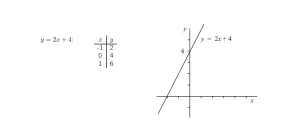Ecuaciones de la recta

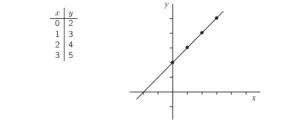
Hay muchos más puntos en la línea, pero ahora tenemos los suficientes para ver un patrón. Si tomamos
cualquier valor de x y le sumamos 2, obtenemos el correspondiente valor de y: 0 + 2 = 2, 1 + 2 = 3, 2 + 2 = 4, y
y así sucesivamente. Existe una relación fija entre las coordenadas x e y de cualquier punto de la recta,
y la ecuación y = x + 2 es siempre cierta para los puntos de la recta. Podemos etiquetar la recta utilizando esta
ecuación.

La ecuación de una línea que pasa por el origen con un determinado gradiente

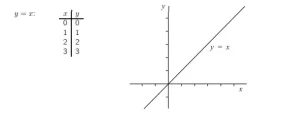
Supongamos que tenemos una recta con ecuación y = x. Entonces, para cada punto de la recta, la coordenada y
debe ser igual a la coordenada x. Por tanto, la recta contendrá los puntos de la siguiente lista.

Podemos encontrar el gradiente de la línea utilizando la fórmula del gradiente

y sustituyendo los dos primeros conjuntos de valores de la tabla. Obtenemos

para que el gradiente de esta recta sea 1.

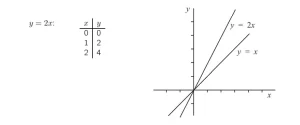
¿Y la ecuación y = 2x? Ésta también representa una recta, y para todos los puntos de la recta cada valor de y es el doble del valor de x correspondiente. Por tanto, la recta contendrá los puntos de la siguiente lista.

Si calculamos el gradiente de la recta y = 2x utilizando los dos primeros conjuntos de valores de la tabla, obtenemos
obtenemos

por lo que el gradiente de esta recta es 2.
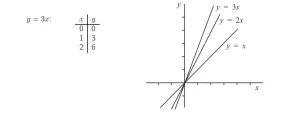
Tomemos ahora la ecuación y = 3x. Esta también representa una línea recta, y para todos los puntos de la
cada valor de y es tres veces el valor de x correspondiente. Por tanto, la recta contendrá los puntos de la
siguiente lista.

Podemos empezar a ver un patrón aquí. Todas estas líneas tienen ecuaciones donde y es igual a algún número
veces x. Y en cada caso la línea pasa por el origen, y el gradiente de la línea está dado por el número que multiplica a x. Así que si tuviéramos una línea con ecuación y = 13x entonces esperaríamos que el gradiente de la línea fuera 13. Del mismo modo, si tuviéramos una recta con ecuación y = -2x entonces el gradiente sería -2. Por lo tanto, en general, la ecuación y = mx representa una línea recta que pasa por el origen con un gradiente m.

La intersección en y de una recta

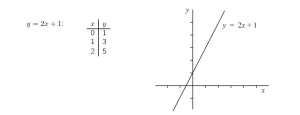
Consideremos la recta con ecuación y = 2x + 1. Esta ecuación tiene una forma ligeramente diferente de las que hemos visto anteriormente. Para dibujar un croquis de la recta, debemos calcular algunos valores.

Observa que cuando x = 0 el valor de y es 1. Por tanto, esta recta corta al eje y en y = 1.

¿Y la recta y = 2x + 4? De nuevo podemos calcular algunos valores.

Esta recta corta el eje y en y = 4.

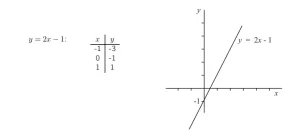
¿Y la recta y = 2x - 1? De nuevo podemos calcular algunos valores.

Esta recta corta al eje y en y = -1.

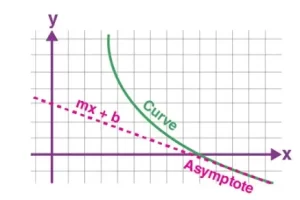
La ecuación general de una recta es y = mx + c, donde m es el gradiente, e y = c es el c es el valor en el que la recta corta al eje y. Este número c se llama intercepción en el eje y.

Vídeos de Ecuaciones de la recta