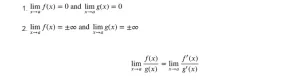Regla de l'hopital

La regla de L'Hospital es un método general para evaluar formas indeterminadas como 0/0 o ∞/∞. Para evaluar los límites de las formas indeterminadas de las derivadas en el cálculo, se utiliza la regla de L'Hospital. La regla de L'Hospital se puede aplicar más de una vez. Se puede aplicar esta regla aún mantiene cualquier forma indeterminada cada vez después de sus aplicaciones. Si el problema está fuera de las formas indeterminadas, no se puede aplicar la regla de L'Hospital.

La regla de L'Hôpital es un teorema utilizado para encontrar el límite de ciertos tipos de formas indeterminadas; las formas indeterminadas son expresiones que resultan de intentar calcular un límite mediante el uso de la sustitución. Por ejemplo, las funciones racionales cuyos límites se evalúan como 0/0 o ∞/∞ se denominan formas indeterminadas, ya que la expresión no proporciona suficiente información para evaluar el límite. Otras formas indeterminadas son 0 - ±∞, ∞ - ∞, 1∞, 00 y ∞0.

Las formas indeterminadas pueden considerarse como una contienda entre los términos de una expresión en la que hay reglas que compiten entre sí y que hacen que no esté claro cuál es el término dominante; esto hace que no esté claro cuál es el límite de la función sin un examen más profundo. Hay varias formas de evaluar los límites (consulte la página de límites para obtener más información). La regla de L'Hôpital sólo se utiliza en los casos en los que un límite es de la forma indeterminada 0/0 o ∞/∞, y el límite no puede calcularse utilizando otros métodos.

Las formas indeterminadas pueden considerarse como una competición entre los términos de una expresión en la que hay reglas que compiten entre sí y que hacen que no esté claro cuál es el término dominante; esto hace que no esté claro cuál es el límite de la función sin un examen más profundo. Hay varias formas de evaluar los límites (consulte la página de límites para obtener más información). La regla de L'Hôpital sólo se utiliza en los casos en que un límite es de la forma indeterminada 0/0 o ∞/∞, y el límite no puede calcularse utilizando otros métodos.

La regla de L'Hôpital es la siguiente: Si f y g son diferenciables y g'(x) ≠ 0 en un intervalo abierto que contenga a (excepto posiblemente en a) y una de las siguientes es cierta,

En otras palabras, la regla de L'Hôpital establece que para las formas indeterminadas del tipo apropiado (0/0 o ∞/∞), el límite puede encontrarse diferenciando ambas expresiones, lo que a menudo da lugar a una expresión simplificada cuyo límite puede calcularse mediante sustitución. Conviene señalar que la regla de L'Hôpital sólo puede utilizarse para estos casos específicos, y no puede utilizarse para calcular todos los límites. Además, en algunos casos, la regla de L'Hôpital debe aplicarse varias veces antes de que el límite pueda calcularse por sustitución; en otros casos, no importa cuántas veces se aplique la regla de L'Hôpital, el resultado seguirá siendo una forma indeterminada, y el límite puede no existir, o puede ser necesario evaluarlo utilizando métodos diferentes.

Otras formas indeterminadas

Aunque la regla de L'Hôpital sólo puede aplicarse a los límites de las formas indeterminadas 0/0 y ∞/∞, a veces es posible reordenar algebraicamente las expresiones para que cumplan los criterios necesarios para utilizar la regla de L'Hôpital.

Vídeos de Regla de l'hopital