Función biyectiva

Funcion biyectiva

En matemáticas, una función biyectiva también se conoce como función de biyección o de correspondencia uno a uno. El término correspondencia uno a uno no debe confundirse con la función uno a uno (es decir, la función inyectiva).

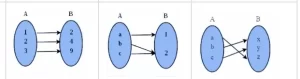
Se dice que una función es biyectiva o biyección, si una función f: A → B satisface las propiedades de función inyectiva (función uno a uno) y función suryectiva (función onto). Esto significa que cada elemento "b" en el codominio B, hay exactamente un elemento "a" en el dominio A. tal que f(a) = b. Si la función satisface esta condición, entonces se conoce como correspondencia uno a uno.

Propiedades de las funciones biyectivas

Una función f: A → B es una función biyectiva si todo elemento b ∈ B y todo elemento a ∈ A, tal que f(a) = b. Se observa que el elemento "b" es la imagen del elemento "a", y el elemento "a" es la preimagen del elemento "b". Las propiedades básicas de la función biyectiva son las siguientes:

Mientras que el mapeo de las dos funciones, es decir, el mapeo entre A y B (donde B no necesita ser diferente de A) para ser una biyección,

cada elemento de A debe estar emparejado con al menos un elemento de B,
ningún elemento de A puede estar emparejado con más de un elemento de B,
cada elemento de B debe estar emparejado con al menos un elemento de A, y
ningún elemento de B puede estar emparejado con más de un elemento de A.

Función inyectiva

Una función que siempre asigna el elemento distinto de su dominio al elemento distinto de su codominio
También se conoce como función uno a uno

Leer Funcion a trozos

Función suryectiva

Función que asigna uno o más elementos de A al mismo elemento de B
También se conoce como función onto