Definición de la derivada

Sea f(x) una función cuyo dominio contiene un intervalo abierto alrededor de algún punto x0. Entonces se dice que la función f(x) es diferenciable en x0, y la derivada de f(x) en x0 viene dada por

Derivada, en matemáticas, tasa de cambio de una función con respecto a una variable. Las derivadas son fundamentales para la solución de problemas de cálculo y ecuaciones diferenciales. En general, los científicos observan sistemas cambiantes (sistemas dinámicos) para obtener la tasa de cambio de alguna variable de interés, incorporan esta información en alguna ecuación diferencial y utilizan técnicas de integración para obtener una función que pueda utilizarse para predecir el comportamiento del sistema original en diversas condiciones.

Las derivadas se definen como la tasa de cambio variable de una función con respecto a una variable independiente. La derivada se utiliza principalmente cuando hay alguna cantidad que varía y la tasa de cambio no es constante. La derivada se utiliza para medir la sensibilidad de una variable (variable dependiente) con respecto a otra variable (variable independiente).

Derivadas en matemáticas - Cálculo

El proceso de encontrar la derivada se llama diferenciación. El proceso inverso se llama antidiferenciación. Vamos a encontrar la derivada de una función y = f(x). Es la medida de la velocidad a la que cambia el valor de y con respecto al cambio de la variable x. Se conoce como la derivada de la función "f", con respecto a la variable x.

Si un cambio infinitesimal en x se denota como dx, entonces la derivada de y con respecto a x se escribe como dy/dx.

Aquí la derivada de y con respecto a x se lee como "dy por dx" o "dy sobre dx"

Ejemplo:

Sea "y" una variable dependiente y "x" una variable independiente.

Consideremos un cambio en el valor de x, es decir, dx.

Este cambio en x provocará un cambio en y, que será dy.

Ahora para encontrar el cambio en y con un cambio unitario en x como sigue:

Sea f(x) una función cuyo valor varía al variar el valor de x

Pasos para encontrar la Derivada:

Cambiar x por el menor valor posible y que sea 'h' y así la función se convierte en f(x+h).
Obtenemos el cambio de valor de la función que es : f(x + h) - f(x)
La tasa de cambio de la función f(x) al pasar de 'x' a 'x+h' será

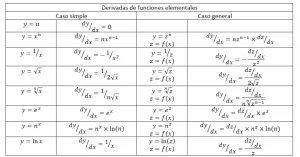
Tabla de derivadas

Tipos de derivadas

Las derivadas se pueden clasificar en diferentes tipos en función de su orden, como las derivadas de primer y segundo orden. Éstas pueden definirse como se indica a continuación.

• Derivada de primer orden
  Las derivadas de primer orden informan sobre la dirección de la función, ya sea creciente o decreciente. La primera derivada matemática o derivada de primer orden puede ser interpretada como una tasa de cambio instantánea. También puede predecirse a partir de la pendiente de la recta tangente.
• Derivada de segundo orden
  Las derivadas de segundo orden se utilizan para tener una idea de la forma de la gráfica de la función dada. Las funciones se pueden clasificar en términos de concavidad. La concavidad de la función de la gráfica dada se clasifica en dos tipos, a saber
  • Cóncava hacia arriba
  • Cóncava hacia abajo

Vídeos de Tabla de derivadas