Distribución normal estándar

Una distribución normal, a veces llamada curva de campana, es una distribución que se da de forma natural en muchas situaciones. Por ejemplo, la curva de campana se observa en exámenes como el SAT y el GRE. El grueso de los estudiantes obtendrá una puntuación media (C), mientras que un número menor de estudiantes obtendrá una B o una D. Un porcentaje aún menor de estudiantes obtendrá una F o una A. Esto crea una distribución que se asemeja a una campana (de ahí el apodo). La curva de campana es simétrica. La mitad de los datos caerán a la izquierda de la media y la otra mitad a la derecha.

Muchos grupos siguen este tipo de patrón. Por eso se utiliza mucho en los negocios, la estadística y en organismos gubernamentales como la FDA:

• La altura de las personas.
• Errores de medición.
• Presión arterial.
• Puntos en un examen.
• Puntuaciones de CI.
• Sueldos.

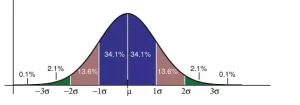
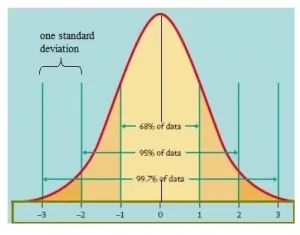
La regla empírica te dice qué porcentaje de tus datos cae dentro de un cierto número de desviaciones estándar de la media:
- El 68% de los datos cae dentro de una desviación estándar de la media.
- El 95% de los datos se encuentra dentro de las dos desviaciones estándar de la media.
- El 99,7% de los datos se encuentra dentro de las tres desviaciones estándar de la media.

La desviación estándar controla la dispersión de la distribución. Una desviación estándar menor indica que los datos están muy agrupados alrededor de la media; la distribución normal será más alta. Una desviación estándar mayor indica que los datos están dispersos alrededor de la media; la distribución normal será más plana y amplia.

Propiedades de una distribución normal

• La media, la moda y la mediana son iguales.
• La curva es simétrica en el centro (es decir, alrededor de la media, μ).
• Exactamente la mitad de los valores están a la izquierda del centro y exactamente la mitad de los valores están a la derecha.
• El área total bajo la curva es 1.

El modelo normal estándar

Un modelo normal estándar es una distribución normal con una media de 0 y una desviación estándar de 1.

Modelo normal estándar: Distribución de los datos

Una forma de averiguar cómo se distribuyen los datos es representarlos en un gráfico. Si los datos se distribuyen uniformemente, se puede obtener una curva de campana. Una curva de campana tiene un pequeño porcentaje de los puntos en ambas colas y el mayor porcentaje en la parte interior de la curva. En el modelo normal estándar, alrededor del 5 por ciento de tus datos caerán en las "colas" (de color naranja más oscuro en la imagen de abajo) y el 90 por ciento estará en el medio. Por ejemplo, en el caso de las puntuaciones de los alumnos en los exámenes, la distribución normal mostraría que el 2,5 por ciento de los alumnos obtienen puntuaciones muy bajas y el 2,5 por ciento muy altas. El resto estará en el medio, ni muy alto ni muy bajo. La forma de la distribución normal estándar es la siguiente:

Vídeos de Distribución normal estándar