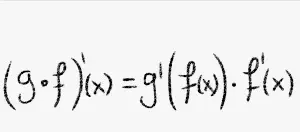Teorema de derivadas

Consideremos una función f (x). La tasa de cambio de la pendiente de la curva de la función dada se llama derivada de la función. El método para encontrar la derivada es la diferenciación. Normalmente, la variable dependiente se representa en términos de la variable independiente. Se denota como dy / dx.

Teoremas importantes sobre la diferenciación

Los siguientes son los teoremas importantes de la diferenciación.

Consideremos dos funciones f (x) y g (x).

• El teorema de Rolle establece que si f es una función que satisface

a. f es continua en el intervalo cerrado [a,b],

b. f es diferenciable en el intervalo abierto (a,b), y

c. f (a) = f (b)

entonces existe un punto c en el intervalo abierto (a,b) tal que f'(c) = 0.

• El teorema del valor medio es una generalización del teorema de Rolle que establece que si f es una función que satisface

a. f es continua en el intervalo cerrado [a,b], y

b. f es diferenciable en el intervalo abierto (a,b),

entonces existe un punto c en el intervalo abierto (a,b) tal que f'(c) = [f(b) - f(a)] / [b-a] donde el lado derecho es la pendiente de la recta que une los puntos (a,f(a)) y (b,f(b)). El Teorema del Valor Medio puede derivarse del Teorema de Rolle considerando la función g(x) = [f(x)] - [(f(b) - f(a)) (x-a) / b-a].

Vídeos de