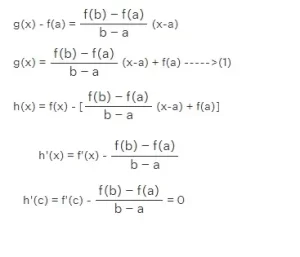Teorema de valor medio
El teorema del valor medio afirma que para una curva que pasa por dos puntos dados hay un punto de la curva en el que la tangente es paralela a la secante que pasa por los dos puntos dados. El teorema de Rolle se ha derivado de este teorema del valor medio.
El teorema del valor medio establece que para una curva f(x) que pasa por dos puntos dados (a, f(a)), (b, f(b)), existe al menos un punto (c, f(c)) en la curva donde la tangente es paralela a la secante que pasa por los dos puntos dados. El teorema del valor medio se define en este caso de cálculo para una función f(x): [a, b] → R, tal que es continua y diferenciable en un intervalo.
- La función f(x) es continua en el intervalo [a, b].
- La función f(x) es diferenciable en el intervalo (a, b). Existe un punto c en (a, b).
Aquí hemos demostrado que la tangente en c es paralela a la secante que pasa por los puntos (a, f(a)), (b, f(b)). Este teorema del valor medio se utiliza para demostrar una afirmación a través de un intervalo cerrado. Además, el teorema de Rolle se deriva de este teorema del valor medio.
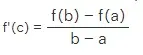
Demostración del teorema del valor medio
Enunciado: El teorema del valor medio establece que si una función f es continua sobre el intervalo cerrado [a,b], y diferenciable sobre el intervalo abierto (a,b), entonces existe al menos un punto c en el intervalo (a,b) tal que f(c) es la tasa de variación media de la función sobre [a,b] y es paralela a la recta secante sobre [a,b].
Demostración: Sea g(x) la recta secante a f(x) que pasa por (a, f(a)) y (b, f(b)). Sabemos que la ecuación de la recta secante es y-y 1 = m (x- x 1 ).
Diferencia entre el teorema del valor medio y el teorema de Rolle
La diferencia entre el teorema del valor medio y el teorema de Rolle ayuda a comprender mejor estos teoremas. Ambos teoremas definen la función f(x) como continua en el intervalo [a, b] y diferenciable en el intervalo (a, b). En el teorema del valor medio, los dos puntos referidos (a, f(a)), (b, f(b)) son distintos y f(a) ≠ f(b). En el teorema de Rolle, los puntos se definen de forma que f(a) = f(b).
El valor de c en el teorema del valor medio se define de forma que la pendiente de la tangente en el punto (c, f(c)) es igual a la pendiente de la secante que une los dos puntos. El valor de c en el teorema de Rolle se define de forma que la pendiente de la tangente en el punto (c, f(c)) es igual a la pendiente del eje x.
