Área de un prisma cuadrangular
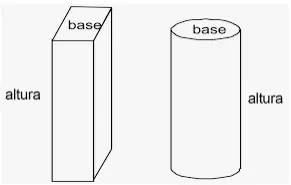
Un prisma cuadrangular es un poliedro, cuyas dos caras de cuadrados iguales se encuentran en planos paralelos, y las restantes caras (caras laterales) son paralelogramos que tienen lados comunes con éstos.
- Un prisma cuadrangular regular es un prisma cuadrangular cuyas bases son cuadrados y las caras laterales son rectángulos.
- Las bases del prisma son iguales a los cuadrados regulares. Las caras laterales del prisma son rectángulos. Las aristas laterales del prisma son paralelas e iguales.
- Las dimensiones del prisma se pueden expresar en términos de la longitud de los lados a y la altura h.
- La superficie total del prisma es igual a su superficie lateral y al área doblada de la base.
- El volumen de un prisma es igual al producto de su altura por el área de la base.
A veces la altura aparece en las tareas. Es perpendicular a las bases. La diagonal de un poliedro es un segmento que une por pares dos vértices cualesquiera que no pertenecen a la misma cara.
Hay que tener en cuenta que el área de la base de un prisma recto o inclinado no depende del ángulo que formen las caras laterales. Si tienen las mismas formas en las aristas superior e inferior, entonces sus áreas serán iguales.
Prisma triangular
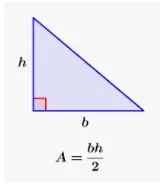
Tiene en su base una figura con tres vértices, es decir, un triángulo. Se sabe que es diferente. Si entonces basta recordar que su área está determinada por la mitad del producto de los catetos.
La notación matemática es la siguiente S = ½ av.
Para averiguar el área de la base en vista general, las fórmulas serán útiles: Heron y aquella en la que se lleva la mitad del lado a la altura trazada a la misma.
La primera fórmula debe escribirse así S = √ (p (p-a) (p-in) (p-c)). Esta entrada contiene un semiperímetro (p), es decir, la suma de tres lados dividida por dos.
Segundo: S = ½ n a * a.
Si se quiere conocer el área del prisma triangular de base, que es regular, entonces el triángulo resulta ser equilátero. Hay una fórmula para ello: S = ¼ a 2 * √3.
Prisma cuadrangular
Su base es cualquiera de los cuadriláteros conocidos. Puede ser un rectángulo o un cuadrado, un paralelepípedo o un rombo. En cada caso, para calcular el área de la base del prisma, necesitarás una fórmula diferente.
Si la base es un rectángulo, su área se determina de la siguiente manera S = ab, donde a, b son los lados del rectángulo.
Cuando se trata de un prisma cuadrangular, el área de la base de un prisma regular se calcula utilizando la fórmula de un cuadrado. Porque es el que resulta estar en la base. S = a 2.
En el caso de que la base sea un paralelepípedo, será necesaria la siguiente igualdad S = a * na. Sucede que el lado del paralelepípedo y uno de los ángulos están dados. Entonces, para calcular la altura, será necesario utilizar una fórmula adicional: n a = b * sen A. Además, el ángulo A es adyacente al lado "b", y la altura es n a opuesta a este ángulo.
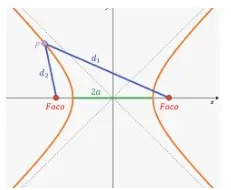
Si hay un rombo en la base del prisma, entonces se necesitará la misma fórmula para determinar su área que para el paralelogramo (ya que es su caso especial). Pero también se puede utilizar ésta: S = ½ d 1 d 2. Aquí d 1 y d 2 son las dos diagonales del rombo.
Prisma pentagonal regular
En este caso hay que dividir el polígono en triángulos, cuyas áreas son más fáciles de averiguar. Aunque ocurre que las figuras pueden ser con distinto número de vértices.
Como la base del prisma es un pentágono regular, se puede dividir en cinco triángulos equiláteros. Entonces el área de la base del prisma es igual al área de uno de esos triángulos (la fórmula se puede ver arriba), multiplicada por cinco.
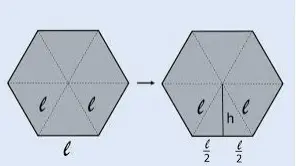
Prisma hexagonal regular
Según el principio descrito para un prisma pentagonal, es posible dividir el hexágono base en 6 triángulos equiláteros. La fórmula del área de la base de dicho prisma es similar a la anterior. Sólo que en ella hay que multiplicar por seis.
La fórmula será la siguiente S = 3/2 y 2 * √3.