Cono

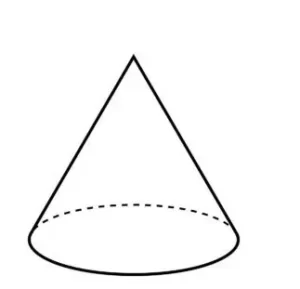
La superficie de un cono es la cantidad de área ocupada por la superficie de un cono. Un cono es una forma tridimensional que tiene una base circular. Esto significa que la base está formada por un radio o diámetro. La distancia entre el centro de la base y la parte superior del cono (por supuesto, en el caso del helado, esta parte está en la parte inferior) es la altura del cono.

¿Qué es la superficie de un cono?

El área ocupada por la superficie/el límite de un cono se conoce como área superficial de un cono. Siempre se mide en unidades cuadradas. Apilando muchos triángulos y girándolos alrededor de un eje se obtiene la forma de un cono. Como tiene una base plana, tiene una superficie total y una superficie curva. Podemos clasificar un cono como cono circular recto o cono oblicuo. El vértice en el cono circular derecho suele estar verticalmente sobre el centro de la base mientras que el vértice del cono en un cono oblicuo no está verticalmente sobre el centro de la base.

Fórmula de la superficie del cono

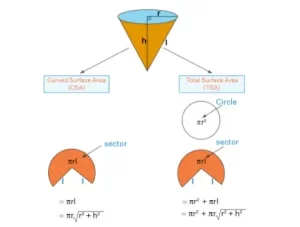
Como un cono tiene una superficie curvada, podemos expresar su área de superficie curvada así como el área de superficie total. Un cono tiene dos tipos de superficie:

Superficie total
Superficie curvada

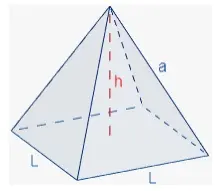
Aplicando el teorema de Pitágoras sobre el cono, podemos encontrar la relación entre la superficie del cono y su altura. Sabemos que, h2 + r2 = l2 donde h es la altura del cono, r es el radio de la base y l es la altura oblicua del cono.
⇒ l = √(h2 + r2)

Por lo tanto,

La superficie total en términos de altura puede darse como, T = πr(r + l) = T = πr(r + √(h2 + r2)).

La superficie curva del cono en términos de altura puede darse como S = πrl = πr(√(h2 + r2)).

Área de la superficie del cono Ejemplo

• ¿Cuál es la altura oblicua del cono si la superficie total del cono es de 616 pulg2 y el radio de 7 pulgadas?

Solución: Las dimensiones dadas son, el área total de la superficie del cono = 616 pulg2 y el radio del cono = 7 pulgadas. Sea la altura de la inclinación = x pulgadas.

Sustituyendo los valores en la fórmula del área de la superficie del cono,
Superficie total del cono = πr (r + l) = (22/7) × 7 × (7 + x) = 616
⇒ 22 × (7 + x) = 616
⇒ 7 + x = 28
⇒ x = 21 pulgadas
Respuesta: La altura inclinada del cono es de 21 pulgadas.

• Cuál es la altura del cono cuyo radio es de 7 pulgadas y la superficie curva es de 550 pulg2 . (Usa π = 22/7)

Solución: Las dimensiones dadas son, radio del cono = 7 in y área de la superficie curva = 550 in2. Sea el valor de la altura de la inclinación "l" y la altura del cono "h".

Sustituyendo los valores en la fórmula de la superficie curva del cono
πrl = (22/7) × 7 × l = 550 pulg2
⇒ 22 × l = 550
⇒ l = 550/22 = 25 pulgadas
l = √(h2 + r2)
⇒ h = √(l2 - r2) = √(252 - 72) = √576 = 24 pulgadas
Respuesta: La altura del cono es de 24 pulgadas.

Vídeos de Cono