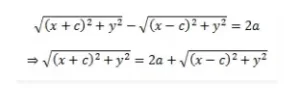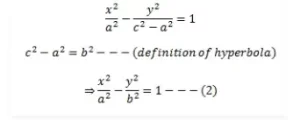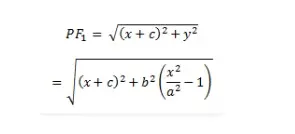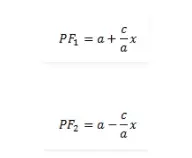Hipérbola

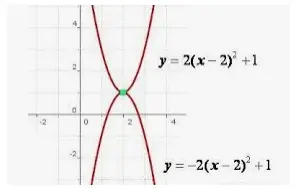
Los puntos fijos se denominan focos (F1 y F2 en la figura anterior) (foco singular). La figura anterior representa una hipérbola tal que P1F2 - P1F1 = P2F2 - P2F1 = P3F1 - P3F2 es una constante.

Cuando ambos focos se unen con la ayuda de un segmento de línea, el punto medio de este segmento de línea que une los focos se conoce como el centro, O representa el centro de una elipse en la figura anterior. El segmento de línea que pasa por ambos focos es el eje transversal de la hipérbola. El segmento de línea perpendicular al eje transversal y que pasa por el centro representa el eje conjugado de la hipérbola.

El punto de intersección de la hipérbola con el eje transversal da los vértices de la hipérbola representados por los puntos A y B en la figura dada. 2a" es la longitud del eje transversal. '2b' es la longitud del eje conjugado. 2c' representa la distancia entre los dos focos. La relación entre a, b y c viene dada por:

b = √(c2 - a2)

Excentricidad de la hipérbola

La relación entre las distancias del centro de la hipérbola de cualquiera de los focos a cualquiera de los vértices de la hipérbola se define como excentricidad.

Excentricidad, e = c/a

Como c ≥ a, la excentricidad es siempre mayor que 1 en el caso de una hipérbola.

Ecuación estándar de la hipérbola

El método más sencillo para determinar la ecuación de una hipérbola es suponer que el centro de la hipérbola está en el origen (0, 0) y los focos se encuentran en el eje x o en el eje y del plano cartesiano, como se muestra a continuación:

Ambos focos se encuentran en el eje x y el centro O se encuentra en el origen.

Consideremos la figura (a) para obtener la ecuación de la hipérbola. Sean las coordenadas de F1 y F2 (-c, 0) y (c, 0) respectivamente como se muestra. Consideremos un punto P(x, y) que se encuentra en la hipérbola y que P satisface la definición, es decir, la diferencia de distancias de P a F1 y F2 en el plano es una constante 2a.

⇒ PF1 - PF2 = 2a - - - (1)

Utilizando la fórmula de la distancia se puede escribir como:

Elevando al cuadrado y simplificando ambos lados obtenemos;

Ahora bien, como P se encuentra en la hipérbola, debe satisfacer la ecuación (2) de forma que 0 < a < c.

Así,

Al simplificar,

Recta de la hipérbola

Los segmentos de línea perpendiculares al eje transversal que pasan por cualquiera de los focos y cuyos puntos extremos se encuentran en la hipérbola se definen como el latus rectum de una hipérbola.

La longitud del latus rectum es 2b2/a.

Vídeos de Hipérbola