Composición de funciones
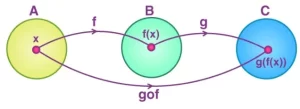
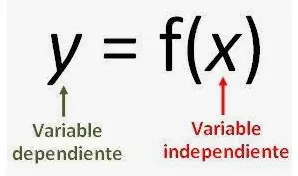
Sean f : A → B y g : B → C dos funciones. Entonces la composición de f y g, denotada por g ∘ f, se define como la función g ∘ f : A → C dada por g ∘ f (x) = g(f (x)), ∀ x ∈ A.
La siguiente figura muestra la representación de las funciones compuestas.
El orden de la función es algo importante cuando se trata de la composición de funciones ya que (f ∘ g) (x) no es igual a (g ∘ f) (x).
La relación y la función es un concepto importante de la clase 11 y 12. Vea a continuación el símbolo de composición de funciones y el dominio con un ejemplo.
Símbolo: También se denota como (g∘f)(x), donde ∘ es un símbolo de círculo pequeño. No podemos sustituir ∘ por un punto (.), porque se mostrará como el producto de dos funciones, como (g.f)(x).
Dominio: f(g(x)) se lee como f de g de x. En la composición de (f o g) (x) el dominio de la función f se convierte en g(x). El dominio es un conjunto de todos los valores que entran en la función.
Ejemplo: Si f(x) = 3x+1 y g(x) = x2 , entonces f de g de x, f(g(x)) = f(x2) = 3x2+1.
Si invertimos la operación de la función, como f de f de x, g(f(x)) = g(3x+1) = (3x+1)2
Propiedades de las composiciones de funciones
Propiedad asociativa: Según la propiedad asociativa de la composición de funciones, si hay tres funciones f, g y h, se dice que son asociativas si y sólo si;
f ∘ (g ∘ h) = (f ∘ g) ∘ h
Propiedad conmutativa: Se dice que dos funciones f y g son conmutativas entre sí, si y sólo si;
g ∘ f = f ∘ g
Algunas propiedades más son:
- La composición de funciones de uno a uno es siempre uno a uno.
- La composición de funciones de dos funciones onto es siempre onto
- La inversa de la composición de dos funciones f y g es igual a la composición de la inversa de ambas funciones, como (f ∘ g)-1 = ( g-1 ∘ f-1).
Cómo se resuelven las funciones compuestas
En matemáticas, resolver una función compuesta significa obtener la composición de dos funciones. Se utiliza un círculo pequeño (∘) para denotar la composición de una función.
Sigue los siguientes pasos para entender cómo resolver la función compuesta dada.
Paso 1: Primero escribe la composición dada de una manera diferente.
Consideremos f(x) = x2 y g(x) = 3x
Ahora,
(f ∘ g) (x) puede escribirse como f[g(x)].
Paso 2: Sustituir la variable x que hay en la función exterior por la función interior tomando como referencia las funciones individuales.
Es decir,
(f ∘ g)(x) = f(3x) {ya que g(x) = 3x}
Paso 3: Por último, simplifica la función obtenida.
(f ∘ g)(x) = f(3x) = (3x)2 {ya que f(x) = x2}
= 9x2
Ejemplo de composición de funciones
Si f (x) = 2x y g(x) = x+1, encuentra (f∘g)(x) si x = 1.
Solución: Dado que f(x) = 2x
g(x) = x+ 1
Por tanto, la composición de f a partir de g será;
(f∘g)(x) = f(g(x)) = f(x+1) = 2(x+1)
Ahora poniendo el valor de x = 1
f(g(1)) = 2(1+1) = 2 (2) = 4
Si f(x) = 2x +1 y g(x) = -x2, encuentra (g∘f)(x) para x = 2.
Solución: Dada,
f(x) = 2x+1
g(x) = -x2
Hallar: g(f(x))
g(f(x)) = g(2x+1) = -(2x+1)2
Ahora pon x =2 para obtener
g(f(2)) = -(2,2+1)2
= -(4+1)2
=-(5)2
=-25
Vídeos de Composición de funciones
Entradas Relacionadas
Contenido