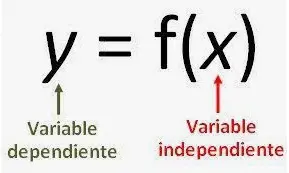
Funciones de primer grado

Una función lineal es cualquier función cuya gráfica es una línea recta. Lo que esto significa matemáticamente es que la función tiene una o dos variables sin exponentes ni potencias. Si la función tiene más variables, éstas deben ser constantes o variables conocidas para que la función siga siendo una función lineal.

Todas las ecuaciones están compuestas por polinomios. Antes sólo hemos mostrado cómo resolver ecuaciones que contienen polinomios de primer grado, pero por supuesto es posible resolver ecuaciones de un grado superior.

Una forma de resolver una ecuación de polinomios es utilizar la propiedad del producto cero. Si recuerdas los capítulos anteriores, la propiedad del cero nos dice que el producto de cualquier número real por el cero es cero. Esto significa que para cualquier número real x e y

six=0 o y=0, entonces xy=0

La propiedad del cero se puede utilizar para resolver una ecuación cuando un lado de la ecuación es un producto de factores polinómicos y el otro lado es cero. Las soluciones de una ecuación polinómica se llaman raíces.

Identificación de funciones lineales

Para identificar las funciones lineales, se puede crear una lista de comprobación de varios elementos que debe cumplir la función.

• El primer elemento que debe satisfacer la función es que debe tener una o dos variables reales. Si hay otra variable, debe ser una variable conocida o una constante. Por ejemplo, la función C = 2 * pi * r es una función lineal porque sólo C y r son variables reales, siendo pi una constante.
• El segundo punto es que ninguna de las variables puede tener un exponente o potencia. No pueden estar al cuadrado, al cubo, o cualquier otra cosa. Todas las variables deben estar en el numerador.
• El tercer punto es que la función debe ser una línea recta. Cualquier tipo de curva descalifica la función.

Por lo tanto, todas las funciones lineales tienen algún tipo de línea recta cuando se grafican. La línea puede ir hacia arriba y hacia abajo, hacia la izquierda y hacia la derecha, o estar inclinada, pero la línea siempre es recta. No importa en qué parte del gráfico se represente la función, siempre que la línea sea recta.

Vídeos de Funciones de primer grado