Derivadas de funciones exponenciales
Hay dos tipos principales de funciones exponenciales: las que modelan el crecimiento exponencial y las que modelan el decaimiento exponencial:
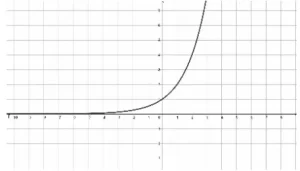
Crecimiento exponencial: Son funciones exponenciales de la forma {eq}f(x) = b^x {/eq} donde {eq}b>1 {/eq}. Son funciones monótonas crecientes, lo que significa que siempre son crecientes en su dominio. En la figura 1 se muestra una función típica de crecimiento exponencial:
Esta función es {eq}f(x) = 2^x {/eq}. Como la base de esta función exponencial es mayor que uno, la función es de crecimiento exponencial.
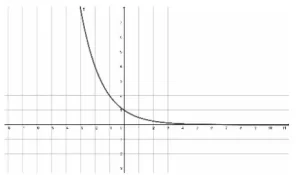
Decaimiento exponencial: Son funciones exponenciales de la forma {eq}f(x) = b^x {/eq} donde {eq}0<b<1 {/eq}. Son funciones monótonas decrecientes, lo que significa que siempre son decrecientes en su dominio. En la figura 2 se muestra una función típica de decrecimiento exponencial:
Esta función es {eq}f(x) = 0,5^x {/eq}. Dado que la base de esta exponencial está entre cero y uno, la función es de decaimiento exponencial.
Por último, la base en la definición de la función exponencial también puede ser negativa. Todo esto hace que se refleje la curva exponencial original sobre el eje x, pero no cambia el tipo de función exponencial.
Derivada de la función exponencial
En primer lugar, la derivada representa la tasa de cambio instantánea de una función (pendiente en cualquier punto de la función). De esta manera, la derivada de la función exponencial representa la tasa de cambio instantánea de la función exponencial. En esencia, la derivada de la función exponencial da una ecuación que produce la pendiente en cualquier punto de la función exponencial.
La fórmula para encontrar la derivada de una función exponencial implica logaritmos, específicamente el logaritmo natural. Por lo tanto, será útil definir primero estos términos y expresiones antes de derivar la derivada de una función exponencial.
El logaritmo es la inversa de la exponencial. Así, si {eq}y=b^x {/eq} es una función exponencial, su inversa viene dada por {eq}y=log_{b}x {/eq}. En esta ecuación, la entrada es x, la salida es y, y la base es b. Una exponencial multiplica un número x de veces una constante de base dada, mientras que el logaritmo determina cuántas veces se multiplica el número de base para obtener algún valor de entrada. Utilizando la ecuación de la definición, el valor de entrada es x. El logaritmo mira cuántas veces se puede multiplicar la base a sí misma para obtener el valor de x. Este valor desconocido es entonces el valor de salida.
Vídeos de Derivadas de funciones exponenciales
Entradas Relacionadas
Contenido