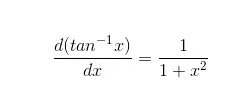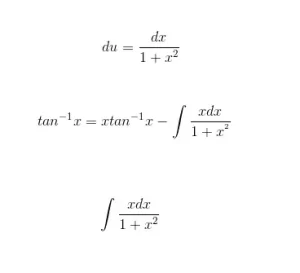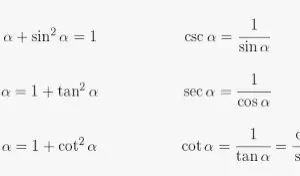Derivadas trigonométricas inversas

Las integrales de las funciones trigonométricas inversas pueden ser difíciles de resolver, ya que los métodos para su integración no son tan sencillos como muchos otros tipos de integrales. Sin embargo, conocer las identidades de las derivadas de estas funciones trigonométricas inversas nos ayudará a derivar sus correspondientes integrales. Por lo tanto, necesitaremos acoplar lo que sabemos en cuanto a las identidades de las derivadas de las funciones trigonométricas inversas con el método de integración por partes para desarrollar fórmulas generales para las integrales correspondientes de estas mismas funciones trigonométricas inversas.

Derivadas de funciones trigonométricas inversas

Es posible que en algún momento hayas visto la siguiente tabla que representa las derivadas de las funciones trigonométricas inversas:

Integración de funciones trigonométricas inversas

Podemos utilizar estas identidades de derivadas trigonométricas inversas junto con el método de integración por partes para derivar fórmulas de integrales para estas funciones trigonométricas inversas.

Usemos la tangente inversa tan-1 x como ejemplo. Dada la fórmula de la derivada de esta función trigonométrica inversa (mostrada en la tabla de derivadas), utilicemos el método de integración por partes, donde ∫ udv = uv - ∫ vdu, para derivar una fórmula correspondiente para la integral de tan-1 x inversa o ∫ tan-1 xdx. Mira de nuevo la derivada de la tangente inversa:

Derivadas de funciones inversas

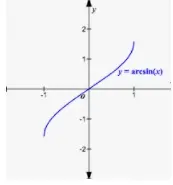
En matemáticas, se dice que una función (por ejemplo, f), es inversa de otra (por ejemplo, g), si dada la salida de g devuelve el valor de entrada dado a f. Además, esto debe ser cierto para cada elemento en el dominio codominio (rango) de g. Por ejemplo suponiendo que x e y son constantes si g(x) = y y f(y) = x entonces se dice que la función f es una inversa de la función g. O en otras palabras, si una función f : A ⇢ B es una - una y una función onto o función biyectiva, entonces una función definida por g : B ⇢ A se conoce como inversa de la función f. La función inversa también se conoce como la anti función. La inversa de la función se denota por f-1.

f(g(x)) = g(f(x)) = x

Vídeos de Derivadas trigonométricas inversas