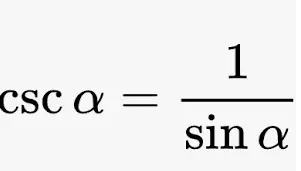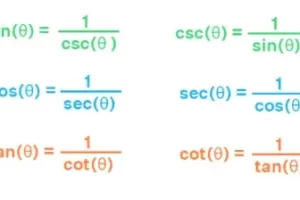Función trigonométrica inversa

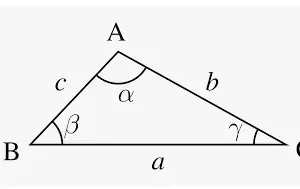
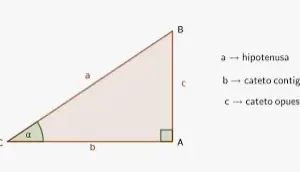
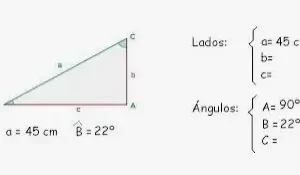
Las funciones trigonométricas inversas también se denominan "funciones de arco" ya que, para un valor determinado de las funciones trigonométricas, producen la longitud de arco necesaria para obtener ese valor concreto. Las funciones trigonométricas inversas realizan la operación contraria de las funciones trigonométricas como el seno, el coseno, la tangente, la cosecante, la secante y la cotangente. Sabemos que las funciones trigonométricas son especialmente aplicables al triángulo rectángulo. Estas seis importantes funciones se utilizan para encontrar la medida del ángulo en el triángulo rectángulo cuando se conocen las medidas de los dos lados del triángulo.

Formulas de Función trigonométrica inversa

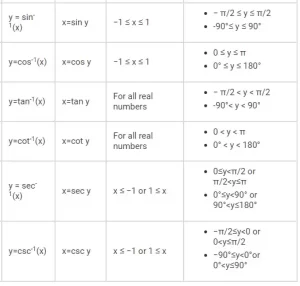
Tabla de funciones trigonométricas inversas

Propiedades de las funciones trigonométricas inversas

Las funciones trigonométricas inversas también se conocen como funciones de arco. Las funciones trigonométricas inversas están definidas en un determinado intervalo (bajo dominios restringidos).

Las propiedades de las funciones trigonométricas inversas se basan en el dominio y el rango de las funciones. Hay algunas propiedades de las funciones trigonométricas inversas que son cruciales no sólo para resolver problemas sino también para tener una comprensión más profunda de este concepto. Para recordar, las funciones trigonométricas inversas también se llaman "funciones de arco". Para un valor dado de una función trigonométrica; producen la longitud de arco necesaria para obtener ese valor particular. El rango de una función inversa se define como el rango de valores de la función inversa que puede alcanzar con el dominio definido de la función. El dominio de una función se define como el conjunto de todas las posibles variables independientes donde existe la función. Las funciones trigonométricas inversas se definen en un intervalo determinado.

Fundamentos de la trigonometría

Los fundamentos de la trigonometría incluyen la trigonometría básica y las razones trigonométricas como sin x, cos x, tan x, cosec x, sec x y cot x.

Gráficas de funciones trigonométricas inversas

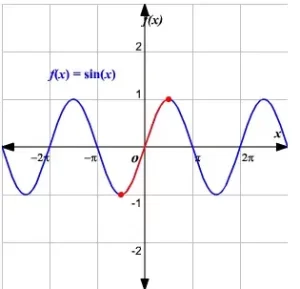
Las funciones trigonométricas son todas funciones periódicas. Por lo tanto, las gráficas de ninguna de ellas pasan la prueba de la línea horizontal y por lo tanto no son 1 - a - 1 . Esto significa que ninguna de ellas tiene una inversa a menos que se restrinja el dominio de cada una de ellas para que sean 1 - a - 1 .

Como las gráficas son periódicas, si elegimos un dominio apropiado podemos utilizar todos los valores del rango .

Si restringimos el dominio de f(x)=sin(x) a [-π/2,π/2] hemos hecho la función 1 a 1 . El rango es [-1,1] .

(Aunque hay muchas formas de restringir el dominio para obtener una función 1 a 1 este es el intervalo acordado que se utiliza).

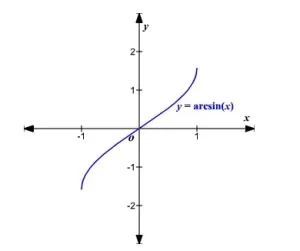
Denotamos la función inversa como y=sin-1(x) . Se lee y es la inversa de seno x y significa que y es el ángulo de número real cuyo valor de seno es x . Tenga cuidado con la notación utilizada. El superíndice " -1 " NO es un exponente. Para evitar esta notación, algunos libros utilizan la notación y=arcsin(x) en su lugar.

Para graficar la inversa de la función seno, recuerda que la gráfica es una reflexión sobre la línea y=x de la función seno.

Observa que el dominio es ahora el rango y el rango es ahora el dominio. Debido a que el dominio está restringido, todos los valores positivos darán un ángulo del primer cuadrante y todos los valores negativos darán un ángulo del cuarto cuadrante.

De manera similar, podemos restringir los dominios de las funciones coseno y tangente para hacerlas 1 a 1 .

Vídeos de Función trigonométrica inversa