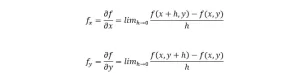Formulas derivadas

Supongamos que tenemos una función f(x, y), que depende de dos variables x e y, donde x e y son independientes entre sí. Entonces decimos que la función f depende parcialmente de x e y. Ahora, si calculamos la derivada de f, entonces esa derivada se conoce como la derivada parcial de f. Si diferenciamos la función f con respecto a x, entonces tomamos y como una constante y si diferenciamos f con respecto a y, entonces tomamos x como una constante.

Símbolo de la derivada parcial

En matemáticas, la derivada parcial de cualquier función que tenga varias variables es su derivada con respecto a una de esas variables manteniendo las demás constantes. La derivada parcial de una función f con respecto a la diferente x se denota de varias maneras por f'x,fx, ∂xf o ∂f/∂x. Aquí ∂ es el símbolo de la derivada parcial.

Ejemplo: Supongamos que f es una función en x e y entonces se expresará por f(x, y). Entonces, la derivada parcial de f respecto a x será ∂f/∂x manteniendo y como constante. Hay que tener en cuenta que es ∂x, no dx. ∂f/∂x también se conoce como fx.

Fórmula de la derivada parcial

Si f(x,y) es una función, donde f depende parcialmente de x e y y si diferenciamos f con respecto a x e y entonces las derivadas se llaman derivada parcial de f. La fórmula de la derivada parcial de f con respecto a x tomando y como constante viene dada por;

Diferenciación parcial

El proceso de encontrar las derivadas parciales de una función dada se llama diferenciación parcial. La diferenciación parcial se utiliza cuando tomamos una de las rectas tangentes de la gráfica de la función dada y obtenemos su pendiente. Vamos a entenderlo con la ayuda del siguiente ejemplo.

Ejemplo:

Supongamos que f es una función de más de una variable tal que

f = x2 + 3xy

La gráfica de z = x2 + 3xy se da a continuación:

La gráfica de esta función representa una superficie en el espacio euclidiano. Para cada punto de esta superficie hay un número infinito de rectas tangentes. Ahora podemos aplicar la diferenciación parcial para elegir una de estas rectas y encontrar su pendiente.

Para encontrar la pendiente de la recta tangente a la función en un punto, digamos P(1,1) y paralela al plano xz, tratamos y como una constante.
Encontrando la derivada de la ecuación tomando y como constante, podemos obtener la pendiente de la función f dada en el punto (x, y). Esto se puede hacer de la siguiente manera.
∂f/∂x = (∂/∂x) (x2 + 3xy) = 2x + 3y
El valor de ∂f/∂x en (1, 1) es:
2(1) + 3(1) = 5
Esto significa que la pendiente es 5.
Por lo tanto, ∂f/∂x = 5 en (1, 1).

Videos de Fórmulas derivadas