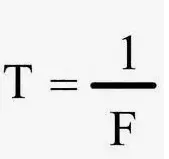Teorema de Bolzano

El Teorema de Bolzano es un caso especial del Teorema de los Valores Intermedios.

También existe el Teorema de Bolzano-Weierstrass (que afirma que todo conjunto infinito acotado de números reales tiene un punto de acumulación).

Las distintas comunidades de matemáticos utilizan a veces nombres diferentes para el mismo teorema o los mismos nombres para teoremas diferentes. En mi limitada experiencia, no he encontrado un "Teorema de Bolzano" diferente.

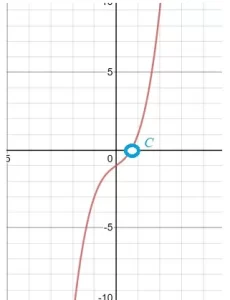
Si una función f en el intervalo cerrado [a, b] ⊂ ℝ → ℝ es una función continua y se cumple que f(a) f(b) < 0, entonces existe al menos un x ∈ (a, b) tal que f(x) = 0

Si no estás familiarizado con la notación

⊂ = subconjunto propio,
∈ = "está en" (es decir, "es un elemento de algún conjunto").
ℝ = El conjunto de los números reales

Dada una función, puedes utilizar el teorema para demostrar que la función tiene al menos una raíz. El teorema no dice nada sobre cuál será el valor del cero de la función: sólo dice que el cero existe.

¿Tiene la ecuación x3 + x - 1 = 0 al menos una solución real en el intervalo cerrado [0, 1]?

En este caso, se ha dado una función (x3 + x - 1) que es cero. Entonces, si la función tiene al menos una solución, esa solución es una raíz (es decir, un cero). Para aplicar el teorema de Bolzano, tienes que averiguar dos cosas:

• ¿Es la función una función continua?
• ¿Los extremos del intervalo tienen signos opuestos?

Paso 1: Comprueba que la función es una función continua. x3 + x - 1 es una función polinómica, por lo que cumple este requisito.

Nota: puedes leer este artículo sobre la comprobación de la continuidad si no estás seguro de cuándo las funciones son continuas (o cuándo no lo son).

Paso 2: Localiza los puntos finales y comprueba si tienen signos opuestos. En este caso, tienes la función y los puntos finales [0, 1], así que introduce los puntos finales en la función y mira qué valores salen:

03 + 0 - 1 = -1
13 + 1 - 1 = 1

Los dos valores tienen signos opuestos, y la función es continua. Por tanto, el teorema de Bolzano nos dice que la ecuación tiene una solución real.

Vídeos de Teorema de Bolzano

https://www.youtube.com/watch?v=zWjcJn3jJjQ