Ley de hooke

En general, para pequeñas deformaciones, la tensión y la deformación son proporcionales entre sí, lo que se conoce como Ley de Hooke.

La ley de Hooke establece que la deformación del material es proporcional a la tensión aplicada dentro del límite elástico de ese material.

Cuando los materiales elásticos se estiran, los átomos y las moléculas se deforman hasta que se aplica la tensión, y cuando se elimina la tensión, vuelven a su estado inicial.

Matemáticamente, la ley de Hooke se expresa como

F = -kx

En la ecuación,F es la fuerza, x es la longitud de extensión, k es la constante de proporcionalidad conocida como constante del muelle en N/m.

La figura muestra el estado estable del muelle cuando no se aplica ninguna carga, el estado del muelle cuando se alarga hasta una cantidad x bajo la carga de 1 N, el estado del muelle alargado hasta 2x bajo la influencia de la carga 2 N.

Dependiendo del material, los diferentes muelles tendrán diferentes constantes de muelle, que se pueden calcular. La figura nos muestra tres casos, la condición estable del resorte, el resorte alargado a una cantidad x bajo una carga de 1 N, y el resorte alargado a 2x bajo una carga de 2 N. Si sustituimos estos valores en la ecuación de la ley de Hooke, obtenemos la constante de resorte para el material en consideración.

Ejemplo resuelto de la ley de Hooke

Un muelle se desplaza 5 cm y se mantiene con una fuerza de 500 N. ¿Cuál es la constante del muelle?

Solución:

Sabemos que el muelle está desplazado 5 cm, pero la unidad de la constante del muelle es Newtons por metro. Esto significa que tenemos que convertir la distancia a metros.

Convirtiendo la distancia a metros, obtenemos

5 cm = 0,05 m

Ahora, sustituyendo los valores en la ecuación, obtenemos

F = -k.x

Ahora, tenemos que rehacer la ecuación para calcular la métrica que falta, que es la constante del muelle, o k. Mirando sólo las magnitudes y, por tanto, omitiendo el signo negativo, obtenemos

500 N/0,05 m = k

k = 10000 N/m

Por lo tanto, la constante del muelle es 10000 N/m.

Gráfica de la Ley de Hooke

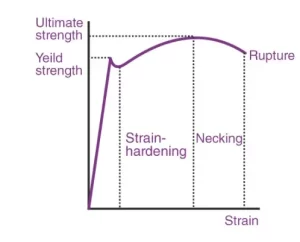
La siguiente figura muestra la curva de tensión-deformación para el acero de bajo carbono.

El material presenta un comportamiento elástico hasta el límite elástico, después de lo cual el material pierde elasticidad y presenta plasticidad.

Desde el origen hasta el límite proporcional cercano al límite elástico, la línea recta implica que el material sigue la ley de Hooke. Más allá del límite elástico entre el límite proporcional y el límite de fluencia, el material pierde su elasticidad y presenta plasticidad. El área bajo la curva desde el origen hasta el límite proporcional cae bajo el rango elástico. El área bajo la curva desde el límite proporcional hasta el punto de ruptura/fractura cae bajo el rango plástico.

La resistencia última del material se define a partir del valor máximo de la ordenada dado por la curva tensión-deformación (desde el origen hasta la ruptura). Este valor proporciona la resistencia a la rotura en un punto de rotura.

En el vídeo se explica la gráfica general de tensión-deformación de un material elástico que experimenta una carga de tracción y cuáles son las distintas etapas de la misma. Dentro del límite elástico sigue la ley de Hooke. A medida que aumentamos la carga, se alcanzan otras etapas y puntos como el límite de proporcionalidad, el límite elástico, el punto de fractura y la resistencia a la tracción final, que se han explicado bien en este vídeo.

Aplicaciones de la Ley de Hooke

A continuación se presentan algunas de las aplicaciones de la Ley de Hooke:

• Se utiliza como principio fundamental en el manómetro, la balanza de resorte, el volante del reloj.
• La ley de Hooke sienta las bases de la sismología, la acústica y la mecánica molecular.

Desventajas de la ley de Hooke

A continuación se exponen algunas de las desventajas de la ley de Hooke:

• La ley de Hooke deja de aplicarse más allá del límite elástico de un material.
• La ley de Hooke es exacta sólo para cuerpos sólidos si las fuerzas y deformaciones son pequeñas.
• La ley de Hooke no es un principio universal y sólo se aplica a los materiales mientras no se estiren más allá de su capacidad

Vídeos de Ley de hooke

https://www.youtube.com/watch?v=w2zTdU0BafI