Máximos y mínimos derivadas

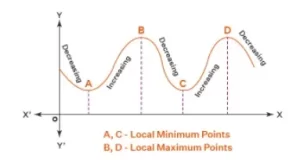
Los máximos y mínimos locales son los valores de entrada para los que la función da los valores de salida máximos y mínimos respectivamente. La ecuación de la función o los gráficos no son lo suficientemente útiles para encontrar los puntos máximos y mínimos locales. La derivada de la función es muy útil para encontrar el máximo y el mínimo local de la función.

Métodos para encontrar el máximo y el mínimo local

El máximo y el mínimo local se pueden identificar tomando la derivada de la función dada. La prueba de la primera derivada y la prueba de la segunda derivada son útiles para encontrar el máximo y el mínimo local. Entendamos más detalles, de cada una de estas pruebas.

Prueba de la primera derivada

La prueba de la primera derivada ayuda a encontrar los puntos de inflexión, donde la salida de la función tiene un valor máximo o un valor mínimo. Para la prueba de la primera derivada. definimos una función f(x) en un intervalo abierto I. Sea la función f(x) continua en un punto crítico c en el intervalo I. Aquí tenemos las siguientes condiciones para identificar el máximo y el mínimo local de la prueba de la primera derivada.

• Si f ′(x) cambia de signo de positivo a negativo a medida que x pasa por c, es decir, si f ′(x) > 0 en todo punto suficientemente cercano y a la izquierda de c, y f ′(x) < 0 en todo punto suficientemente cercano y a la derecha de c, entonces c es un punto de máximo local.
• Si f ′(x) cambia de signo de negativo a positivo a medida que x pasa por c, es decir, si f ′(x) < 0 en cada punto suficientemente cercano y a la izquierda de c, y f ′(x) > 0 en cada punto suficientemente cercano y a la derecha de c, entonces c es un punto de mínimos locales.
• Si f ′(x) no cambia significativamente a medida que x pasa por c, entonces c no es un punto de máximos locales ni un punto de mínimos locales. De hecho, dicho punto se denomina punto de inflexión.

Los siguientes pasos son útiles para completar la prueba de la primera derivada y encontrar los puntos límite.

• Encuentre la primera derivada de la función dada, y encuentre los puntos límite igualando la expresión de la primera derivada a cero.
• Encuentre un punto en el lado izquierdo vecino y en el lado derecho vecino del punto límite, y sustituya estos puntos vecinos en las funciones de la primera derivada.
• Si la derivada de la función es positiva para el punto vecino de la izquierda, y es negativa para el punto vecino de la derecha, entonces el punto límite es el máximo local.
• Si la derivada de la función es negativa para el punto vecino de la izquierda, y es positiva para el punto vecino de la derecha, entonces el punto límite es el mínimo local.

Prueba de la segunda derivada

La prueba de la segunda derivada es un método sistemático para encontrar el valor máximo y mínimo absoluto de una función de valor real definida en un intervalo cerrado o acotado. Consideramos una función f(x) que es diferenciable dos veces y está definida en un intervalo cerrado I, y un punto x= k que pertenece a este intervalo cerrado (I). Aquí tenemos las siguientes condiciones para identificar el máximo y el mínimo local a partir de la prueba de la segunda derivada.

• x = k, es un punto de máximo local si f'(k) = 0, y f''(k) < 0. El punto en x= k es el máximo local y f(k) se llama el valor máximo local de f(x).
• x = k es un punto de mínimo local si f'(k) = 0, y f''(k) >0 . El punto en x = k es el mínimo local y f(k) se llama valor mínimo local de f(x).
• La prueba falla si f'(k) = 0, y f''(k) = 0. Y el punto x = k se llama punto de inflexión.

Vídeos de Máximos y mínimos derivadas