Rango intercuartil

La fórmula del rango intercuartil es el primer cuartil restado del tercer cuartil:

IQR = Q3 - Q1.

El rango intercuartil (IQR) mide la dispersión de la mitad de los datos. Es el rango del 50% medio de la muestra. Utilice el IQR para evaluar la variabilidad en la que se encuentra la mayoría de sus valores. Los valores más grandes indican que la parte central de sus datos se dispersa más. Por el contrario, los valores más pequeños muestran que los valores centrales se agrupan más estrechamente.

Visión general del rango intercuartílico

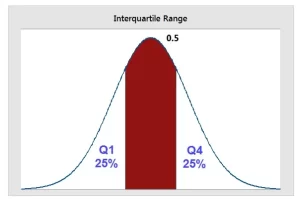
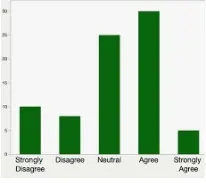
Para visualizar el rango intercuartil, imagine que divide sus datos en trimestres. Los estadísticos se refieren a estos trimestres como cuartiles y los etiquetan de menor a mayor como Q1, Q2, Q3 y Q4. El cuartil más bajo (Q1) abarca el trimestre más pequeño de valores en su conjunto de datos. El cuartil superior (Q4) comprende el trimestre más alto de valores. El rango intercuartil es la mitad de los datos que se encuentra entre los cuartiles superior e inferior. En otras palabras, el rango intercuartil incluye el 50% de los puntos de datos que están por encima del Q1 y por debajo del Q4. El IQR es el área roja en el gráfico de abajo, que contiene Q2 y Q3 (no etiquetados).

Al medir la variabilidad, los estadísticos prefieren utilizar el rango intercuartil en lugar del rango completo de los datos porque los valores extremos y los valores atípicos le afectan menos. Normalmente, se utiliza el IQR con una medida de tendencia central, como la mediana, para comprender el centro y la dispersión de los datos. Esta combinación crea una imagen más completa de la distribución de los datos.

A diferencia de la media y la desviación estándar, más conocidas, el rango intercuartil y la mediana son medidas robustas. Los valores atípicos no influyen mucho en ninguna de las dos estadísticas porque no dependen de cada valor. Además, al igual que la mediana, el rango intercuartil es magnífico para las distribuciones sesgadas. En el caso de las distribuciones normales, se puede utilizar la desviación estándar para determinar el porcentaje de observaciones que se encuentran a distancias específicas de la media. Sin embargo, eso no funciona para las distribuciones sesgadas, y el IQR es una excelente alternativa.

¿Qué es la fórmula del rango intercuartil?

La fórmula del Rango Intercuartil (IQR) es una medida del 50% medio de un conjunto de datos. La más pequeña de todas las medidas de dispersión en estadística se llama Rango Intercuartil. La diferencia entre el cuartil superior y el inferior se conoce como rango intercuartil.

Fórmula IQR

Rango intercuartil = Cuartil superior - Cuartil inferior

Q2=Q3-Q1

donde,

IQR = Rango intercuartil (IQR = Q2)

Q1= (1/4)[(n + 1)]º término)

Q3= (3/4)[(n + 1)]º término)

n = número de puntos de datos

Los siguientes pasos nos ayudan a encontrar el IQR:

El sencillo truco consiste en ordenar los puntos de datos en orden ascendente.
Q 2 es la mediana de los datos. Si el número de puntos de datos es impar, el término medio es (n+1)/2 y si el número de puntos de datos es par, la mediana es la media de los dos puntos medios.
Q 1 es la mediana de los puntos de datos situados a la izquierda de la mediana hallada en el paso 2.
Q 3 es la mediana de los puntos de datos a la derecha de la mediana encontrada en el paso 2.

IQR = Q 2 = Q 3 - Q 1

Vídeos de Rango intercuartil