Razones trigonométricas

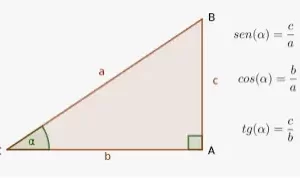
En este diagrama, tienes un triángulo rectángulo del que conoces la longitud de un lado y la medida de un ángulo agudo. Quieres encontrar la longitud de la hipotenusa. Ya sabes que el Teorema de Pitágoras te permite encontrar la longitud de un lado de un triángulo rectángulo, dadas las longitudes de los otros dos lados. Ahora aprenderás trigonometría, que es una rama de las matemáticas que estudia la relación entre los ángulos y los lados de los triángulos. De hecho, la trigonometría te permitirá encontrar las longitudes de los lados y las medidas de los ángulos desconocidos en los triángulos rectángulos en una variedad de casos, como en el problema anterior.

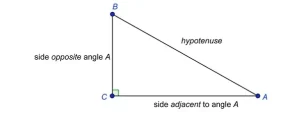
Los lados de un triángulo rectángulo

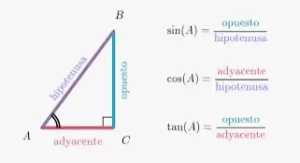
En el ejemplo anterior, uno de los ángulos agudos tiene una medida de 20°. Se podría describir el lado (o cateto del triángulo rectángulo) con una longitud de 4 pies como la altura del triángulo, o se podría decir que es "opuesto" al ángulo de 20°. El otro cateto se dice que es "adyacente" al ángulo de 20°. En trigonometría, este tipo de relación entre lados y ángulos es muy importante.

La relación general entre lados y ángulos se muestra en el siguiente diagrama.

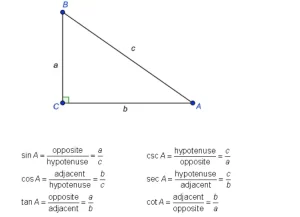
Las seis razones trigonométricas

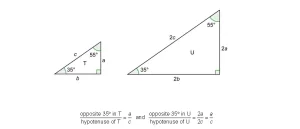
Supón que tu profesor os pide a ti y a otro estudiante que dibujéis un triángulo con medidas de ángulo de 35°, 55° y 90°. Es probable que tú y tu amigo dibujéis triángulos de tamaños diferentes. Sin embargo, como los triángulos tendrán las mismas medidas de ángulo, serán similares.

Recuerda que esto significa que los triángulos tendrán lados correspondientes proporcionales. Por ejemplo, un triángulo puede tener lados que sean el doble de largos que los lados del otro, como se ve a continuación.

Las definiciones son las siguientes:

Vídeos de Razones trigonométricas