Matriz triangular superior

Una matriz cuadrada cuyos elementos por encima de la diagonal principal son cero se llama matriz triangular inferior.
Una matriz cuadrada cuyos elementos por debajo de la diagonal principal son cero se denomina matriz triangular superior.

¿Qué es una matriz triangular?

Una matriz triangular es un tipo especial de matriz cuadrada en el conjunto de las matrices. Hay dos tipos de matrices triangulares: matriz triangular inferior y matriz triangular superior.

• Se dice que una matriz cuadrada es una matriz triangular inferior si todos los elementos por encima de su diagonal principal son cero.
• Se dice que una matriz cuadrada es una matriz triangular superior si todos los elementos por debajo de la diagonal principal son cero.

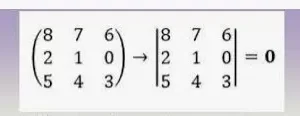
A continuación se presenta un ejemplo de matriz triangular:

Tipos de matrices triangulares

Existen diferentes tipos de matrices triangulares que estudiamos. A continuación se presenta una lista de algunos tipos especiales de matrices triangulares:

• Matriz Triangular Superior: Se dice que una matriz triangular es una matriz triangular superior si todos los elementos por debajo de la diagonal principal son cero.
• Matriz triangular inferior: Se dice que una matriz triangular es una matriz triangular inferior si todos los elementos por encima de la diagonal principal son cero.
• Matriz estrictamente triangular: Se dice que una matriz triangular es una matriz estrictamente triangular si todos los elementos de la diagonal principal son cero.
• Matriz estrictamente triangular inferior: Se dice que una matriz triangular inferior es una matriz estrictamente triangular inferior si todos los elementos de la diagonal principal son cero.
• Matriz estrictamente triangular superior: Se dice que una matriz triangular superior es una matriz estrictamente triangular superior si todos los elementos de la diagonal principal son cero.
• Matriz triangular unitaria: Se dice que una matriz triangular es una matriz triangular unitaria si todos los elementos de la diagonal principal son iguales a 1.
• Matriz triangular inferior unitaria: Se dice que una matriz triangular inferior es una matriz triangular inferior unitaria si todos los elementos de la diagonal principal son iguales a 1.
• Matriz triangular superior unitaria: Se dice que una matriz triangular superior es una matriz triangular superior unitaria si todos los elementos de la diagonal principal son iguales a 1.

Matriz triangular superior

Se dice que una matriz cuadrada n × n A = [aij] es una matriz triangular superior si y sólo si aij = 0, para todo i > j. Esto implica que todos los elementos por debajo de la diagonal principal de una matriz cuadrada son cero en una matriz triangular superior. Una notación general de una matriz triangular superior es U = [uij para i ≤ j, 0 para i > j].

Propiedades de la matriz triangular

Ya que hemos entendido el significado de una matriz triangular, repasemos algunas de sus propiedades importantes. A continuación se muestra una lista de las propiedades de una matriz triangular:

• La transposición de una matriz triangular es triangular.
• La transposición de una matriz triangular inferior es n matriz triangular superior y viceversa.
• El producto de dos matrices triangulares es una matriz triangular.
• Una matriz triangular es invertible si y sólo si todas las entradas de la diagonal principal son distintas de cero.
• El producto de dos matrices triangulares inferiores(superiores) es una matriz triangular inferior(superior).
• La inversa de una matriz triangular es triangular.
• El determinante de una matriz triangular es el producto de los elementos de la diagonal principal.

Vídeos de Matriz triangular superior