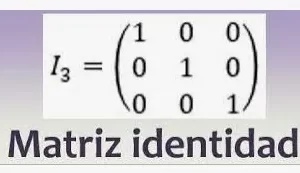
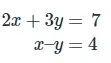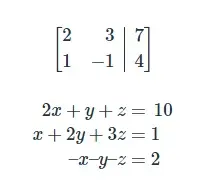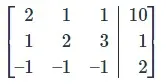Método de gauss Jordán

La eliminación gaussiana es un método estructurado para resolver un sistema de ecuaciones lineales. Por lo tanto, es un algoritmo y puede programarse fácilmente para resolver un sistema de ecuaciones lineales. El objetivo principal de la eliminación de Gauss-Jordan es:

• representar un sistema de ecuaciones lineales en forma de matriz aumentada
• luego realizar las 3 operaciones de fila en ella hasta conseguir la forma escalonada de fila reducida (RREF)
• Por último, podemos reconocer fácilmente las soluciones a partir de la RREF

Matriz aumentada

A continuación se muestra un sistema de ecuaciones lineales:

Escribiremos la matriz aumentada de este sistema utilizando los coeficientes de las ecuaciones y escribiéndola en el estilo que se muestra a continuación:

Operaciones de fila en una matriz

Hay 3 operaciones elementales de fila que podemos hacer en las matrices. No cambiarán la solución del sistema. Son:

• Intercambiar 2 filas
• Multiplicar una fila por un escalar no nulo ()
• Sumar o restar el múltiplo escalar de una fila a otra fila.

Forma escalonada reducida

El objetivo principal de la eliminación de Gauss Jordan es utilizar las operaciones 3  elementales de fila en una matriz aumentada para reducirla a la forma escalonada reducida (RREF). Se dice que una matriz está en forma escalonada reducida, también conocida como forma canónica, si se cumplen las siguientes condiciones:

• Las filas con entradas nulas (todos los elementos de esa fila son s) están en la parte inferior de la matriz.
• La entrada principal (la primera entrada no nula de una fila) de cada fila no nula está a la derecha de la entrada principal de la fila que está justo encima.
• La entrada principal de cualquier fila no nula es 1.
• Todas las entradas de la columna que contiene la entrada principal (1) son ceros.

Cómo hacer la eliminación de Gauss Jordan

No hay pasos definidos para el Método de Eliminación de Gauss Jordan, pero el algoritmo que sigue describe los pasos que realizamos para llegar a la forma escalonada reducida de la matriz aumentada.

• Intercambiar filas para que todas las filas con entradas cero estén en la parte inferior de la matriz.
• Intercambiar las filas para que la fila con el mayor dígito a la izquierda esté en la parte superior de la matriz.
• Multiplica la fila superior por un escalar que convierta la entrada principal de la fila superior en 1(Si la entrada principal de la fila superior es , entonces multiplícala por para obtener ).
• Sume o reste los múltiplos de la fila superior a las otras filas para que las entradas de la columna de la entrada principal de la fila superior sean todas ceros.
• Realice los pasos para la siguiente entrada no nula de la izquierda hasta que todas las entradas principales de cada fila sean  1.
• Intercambie las filas de modo que la entrada principal de cada fila distinta de cero esté a la derecha de la entrada principal de la fila directamente superior.

Vídeos de Método de Gauss Jordán