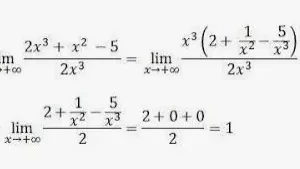Tipo de funciones

La función y = f(x) se clasifica en diferentes tipos de funciones, basándose en factores como el dominio y el rango de una función, y la expresión de la función. Las funciones tienen un valor de dominio x que se denomina entrada. El valor del dominio puede ser un número, un ángulo, un decimal o una fracción. Del mismo modo, el valor y o el valor f(x) (generalmente es un valor numérico) es el rango. Los tipos de funciones se han clasificado en los siguientes cuatro tipos.

• Basadas en los elementos del conjunto
• Basadas en la Ecuación
• Basadas en el Rango
• Basadas en el Dominio

Representación de las funciones

Existen tres formas diferentes de representación de las funciones. Las funciones necesitan ser representadas para mostrar los valores del dominio y los valores del rango y la relación entre ellos. Las funciones pueden representarse con la ayuda de diagramas de Venn, formatos gráficos y formas de listas. Los detalles de cada una de las formas de representación son los siguientes.

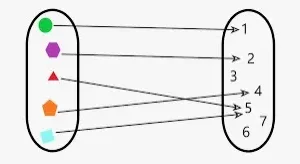
• Diagrama de Venn: El diagrama de Venn es un formato importante para representar la función. Los diagramas de Venn suelen presentarse como dos círculos con flechas que conectan el elemento en cada uno de los círculos. El dominio se presenta en un círculo y los valores del rango se presentan en otro círculo. Y la función define las flechas, y cómo las flechas conectan los diferentes elementos en los dos círculos.
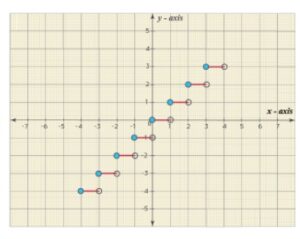
• Forma gráfica: Las funciones son fáciles de entender si se representan en forma gráfica con la ayuda de los ejes de coordenadas. Representar la función en forma gráfica, nos ayuda a entender el comportamiento cambiante de las funciones si la función es creciente o decreciente. El dominio de la función - el valor x se representa a lo largo del eje x, y el rango o el valor f(x) de la función se representa con respecto al eje y.
• Forma de lista: La notación de lista de un conjunto es una representación matemática simple del conjunto en forma matemática. El dominio y el rango de la función se representan entre paréntesis con el primer elemento de un par que representa el dominio y el segundo elemento que representa el rango. Intentemos entenderlo con la ayuda de un ejemplo sencillo. Para una función de la forma f(x) = x2, la función se representa como {(1, 1), (2, 4), (3, 9), (4, 16)}. Aquí el primer elemento es el dominio o el valor de x y el segundo elemento es el rango o el valor de f(x) de la función.

Tipos de Funciones - Basadas en los Elementos del Conjunto

Estos tipos de funciones se clasifican en función del número de relaciones entre los elementos del dominio y el codominio. Los diferentes tipos de funciones basadas en elementos del conjunto son los siguientes.

• Función uno a uno
  Una función uno a uno se define por f: A → B tal que cada elemento del conjunto A está conectado a un elemento distinto del conjunto B. La función uno a uno también se llama función inyectiva. Aquí cada elemento del dominio tiene una imagen distinta o elemento codominio para la función dada.
• Función de muchos a uno
  Una función muchos a uno se define por la función f: A → B, tal que más de un elemento del conjunto A está conectado al mismo elemento del conjunto B. En una función muchos a uno, más de un elemento tiene el mismo codominio o imagen. Si una función muchos a uno, en el codominio, es un solo valor o el elemento del dominio están todos conectados a un solo elemento, entonces se llama una función constante.
• Función Onto
  En una función onto, cada elemento del codominio está relacionado con el elemento del dominio. Para una función definida por f: A → B, tal que cada elemento del conjunto B tiene una preimagen en el conjunto A. La función onto también se llama función subjetiva.
• Función uno y onto (biyección)
  Una función que es a la vez una función uno y onto se llama función biyectiva. Aquí cada elemento del dominio está conectado a un elemento distinto en el codominio y cada elemento del codominio tiene una preimagen. También, en otras palabras, cada elemento del conjunto A está conectado a un elemento distinto del conjunto B, y no hay ningún elemento del conjunto B que haya quedado fuera.
• Función Into
  La función into es exactamente lo contrario a una función onto. Aquí hay ciertos elementos en el codominio que no tienen ninguna preimagen. Los elementos del conjunto B son excesivos y no están conectados con ningún elemento del conjunto A.
• Función constante
  Una función constante es una forma importante de una función de muchos a uno. En una función constante, todos los elementos del dominio tienen una sola imagen. La función constante es de la forma f(x) = K, donde K es un número real. Para los diferentes valores del dominio(valor de x), se obtiene el mismo valor de rango de K para una función constante.

Tipos de funciones - Basadas en la ecuación

Las expresiones algebraicas también son funciones y se basan en el grado del polinomio. Las funciones basadas en ecuaciones se clasifican en las siguientes ecuaciones basadas en el grado de la variable 'x'.

• • La función polinómica de grado cero se llama función constante.
  • La función polinómica de grado uno se llama Función Lineal.
  • La función polinómica de grado dos se llama Función Cuadrática.
  • La función polinómica de grado tres es una Función Cúbica.
• Función de identidad
  La función identidad tiene el mismo dominio y rango. La ecuación de la función identidad es f(x) = x, o y = x. El dominio y el rango de la función identidad son de la forma {(1, 1), (2, 2), (3, 3), (4, 4).....(n, n)}. La gráfica de la función identidad es una recta igualmente inclinada respecto a los ejes de coordenadas y que pasa por el origen. La función identidad puede tomar tanto valores positivos como negativos y por tanto está presente en el primer y tercer cuadrante del eje de coordenadas.
• Función lineal
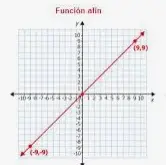
  Una función polinómica cuya ecuación es de primer grado es una función lineal. El dominio y el rango de una función lineal es un número real, y tiene una gráfica de línea recta. Ecuaciones como y = x + 2, y = 3x, y = 2x - 1, son todos ejemplos de funciones lineales. La función identidad de y = x también puede considerarse una función lineal. La forma general de una función lineal es f(x) = ax + b, se utiliza para representar funciones objetivo en problemas de programación lineal. Aquí x, y son variables, y a, b son números reales. Gráficamente para representar la función lineal se puede representar por la ecuación de una línea y = mx + c, donde m es la pendiente de la línea y c es la intersección de la línea.
• Función cuadrática
  Una función cuadrática tiene una ecuación cuadrática de segundo grado y tiene una gráfica en forma de curva. La forma general de la función cuadrática es f(x) = ax2 + bx + c, donde a ≠ 0 y a, b, c son constantes y x es una variable. El dominio y el rango de la función cuadrática es R. La gráfica de una ecuación cuadrática es una gráfica no lineal y tiene forma parabólica. Ejemplos de funciones cuadráticas son f(x) = 3x2 + 5, f(x) = x2 - 3x + 2.
• Función cúbica
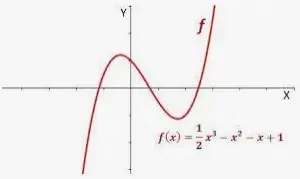
  Una función cúbica tiene una ecuación de grado tres. La forma general de una función cúbica es f(x) = ax3 + bx2 + cx +d, donde a ≠ 0 y a, b, c y d son números reales y x es una variable. El dominio y el rango de una función cúbica es R. La gráfica de una función cúbica es más curva que la de una función cuadrática. Un ejemplo de función cúbica es f(x) = 8x3 + 5x2 + 3.
• Función polinómica
  La forma general de una función polinómica es f(x) = anxn + an-1xn-1 + an-2xn-2+ ..... ax + b. Aquí n es un número entero no negativo y x es una variable. El dominio y el rango de una función polinómica son R. Basándose en la potencia de la función polinómica, las funciones pueden clasificarse como función cuadrática, función cúbica, etc.

Tipos de funciones - Según el rango

Aquí se han clasificado los tipos de funciones basándose en el rango que se obtiene de las funciones dadas. Los diferentes tipos de funciones basados en el rango son los siguientes.

• Función Modulo
  La función módulo da el valor absoluto de la función, independientemente del signo del valor del dominio de entrada. La función módulo se representa como f(x) = |x|. El valor de entrada de 'x' puede ser una expresión positiva o negativa. La gráfica de una función módulo se encuentra en el primer y segundo cuadrante ya que las coordenadas de los puntos de la gráfica son de la forma (x, y), (-x, y).
• Función racional
  Una función compuesta por dos funciones y expresada en forma de fracción es una función racional. Una fracción racional es de la forma f(x)/g(x), y g(x) ≠ 0. Las funciones utilizadas en esta función racional pueden ser una función algebraica o cualquier otra función. La representación gráfica de estas funciones racionales es similar a la de las asíntotas, ya que no toca las líneas del eje.
• Función Signum
  La función signo nos ayuda a conocer el signo de la función y no da el valor numérico ni ningún otro valor para el rango. El rango de la función signo está limitado a {-1, 0, 1}. Para el valor positivo del dominio, la función signum da una respuesta de 1, para los valores negativos la función signum da una respuesta de -1, y para el valor 0 de un dominio, la imagen es 0. La función signum tiene una amplia aplicación en la programación de software.

La gráfica de la función entera mayor se conoce como curva escalonada debido a la estructura escalonada de la curva.La función integral mayor se denota como f(x) = ⌊x⌋. Para una función que toma valores de [1, 2), el valor de f(x) es 1.

Función compuesta
Las funciones compuestas son de la forma de gof(x), fog(x), h(g(f(x)), y está hecha a partir de las funciones individuales de f(x), g(x), h(x). Las funciones compuestas hechas a partir de dos funciones tienen el rango de una función formando el dominio para otra función. Consideremos una función compuesta fog(x), que está formada por dos funciones f(x) y g(x). Aquí escribimos fog(x) = f(g(x)). El rango de g(x) constituye el dominio de la función f(x). Se puede considerar como una secuencia de dos funciones. Si f(x) = 2x + 3 y g(x) = x + 1 tenemos que fog(x) = f(g(x)) = f(x + 1) = 2(x + 1) + 3 = 2x + 5.

Tipos de funciones - Según el dominio

Las funciones se utilizan en todos los demás temas de las matemáticas. Las funciones se han clasificado en función de los tipos de ecuaciones que se utilizan para definirlas. Las ecuaciones de las funciones generalmente tienen expresiones algebraicas, funciones trigonométricas, logaritmos, exponentes, y por lo tanto se denominan en base a estos valores de dominio. Los tres grandes tipos de funciones basados en el valor del dominio son los siguientes.

• Función algebraica
  Una función algebraica es útil para definir las diversas operaciones del álgebra. La función algebraica tiene una variable, un coeficiente, un término constante y varios operadores aritméticos como la suma, la resta, la multiplicación y la división. Una función algebraica suele tener la forma de f(x) = anxn + an - 1xn - 1+ an-2xn-2+ ....... ax + c. La función algebraica también puede representarse gráficamente. La función algebraica también se denomina función lineal, función cuadrática, función cúbica, función polinómica, según el grado de la ecuación algebraica.
• Funciones trigonométricas
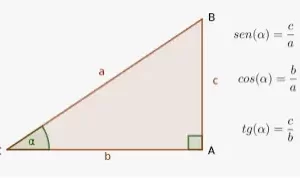
  Las funciones trigonométricas también tienen un dominio y un rango similares a los de cualquier otra función. Las seis funciones trigonométricas son f(θ) = sinθ, f(θ) = cosθ, f(θ) = tanθ, f(θ) = secθ, f(θ) = cosecθ. Aquí el valor del dominio θ es el ángulo y está en grados o en radianes. Estas funciones trigonométricas se han tomado a partir de la razón de los lados de un triángulo rectángulo, y se basan en el teorema de Pitágoras. Además de estas funciones trigonométricas, también se han derivado funciones trigonométricas inversas. El dominio de la función trigonométrica inversa es un valor numérico real y su rango es un ángulo. Las funciones trigonométricas y las funciones trigonométricas inversas también se denominan a veces funciones periódicas, ya que los valores principales se repiten.
• Funciones logarítmicas
  Las funciones logarítmicas se han derivado de las funciones exponenciales. Las funciones logarítmicas se consideran la inversa de las funciones exponenciales. Las funciones logarítmicas tienen un "log" en la función y tienen una base. La función logarítmica es de la forma y = log a x . Aquí el valor del dominio es el valor de entrada de 'x' y se calcula utilizando la tabla logarítmica de Napier. La función logarítmica da el número de veces exponencial al que se ha elevado la base para obtener el valor de x. La misma función logarítmica puede expresarse como función exponencial como x = ay.

Vídeos de Tipo de funciones