Algebra

Función afín

Función afín
Las funciones y las relaciones son uno de los temas más importantes del álgebra. En la mayoría de las ocasiones, mucha gente tiende a confundir el significado de estos dos términos. En este artículo, definiremos y elaboraremos cómo se puede identificar si una relación es una función. Antes de profundizar, veamos una breve historia de las funciones. El concepto de función fue dado a conocer por los matemáticos en el siglo XVII. En 1637, el matemático y primer filósofo moderno, René Descartes, habló de muchas relaciones matemáticas en su libro Geometría. Sin embargo, el término «función» fue utilizado oficialmente por primera vez por el matemático alemán Gottfried Wilhelm Leibniz después de unos cincuenta años. Inventó una notación y = x para denotar una función, dy/dx, para denotar la derivada de una función. La notación y = f (x) fue introducida por el matemático suizo Leonhard Euler en 1734.

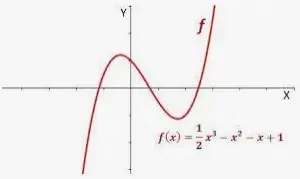
Función afín

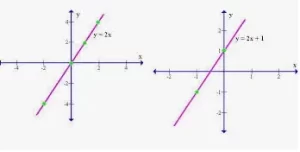
En matemáticas, una función puede definirse como una regla que relaciona cada elemento de un conjunto, llamado dominio, con exactamente un elemento de otro conjunto, llamado rango. Por ejemplo, y = x + 3 e y = x2 - 1 son funciones porque cada valor de x produce un valor de y diferente.

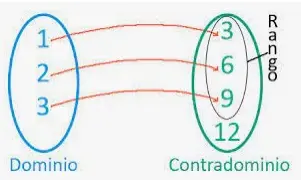
¿Qué es un dominio?

Un dominio es un conjunto de todos los valores de entrada o primeros valores de una función. Los valores de entrada son generalmente los valores "x" de una función.

¿Qué es un rango?

El rango de una función es un conjunto de todos los valores de salida o segundos valores. Los valores de salida son los valores "y" de una función.

Tipos de funciones

Las funciones se pueden clasificar en función de sus relaciones de la siguiente manera

  • Función inyectiva o unívoca: La función inyectiva f: P → Q implica que existe un elemento distinto de Q por cada elemento de P.
  • De muchos a uno: La función muchos a uno mapea dos o más elementos de P al mismo elemento del conjunto Q.
  • La función suryectiva o onto: Es una función para la que cada elemento del conjunto Q tiene una preimagen en el conjunto P
  • La función biyectiva.
Leer  Matriz simétrica

Las funciones comunes en el álgebra son

  • Función lineal
  • Funciones inversas
  • Función constante
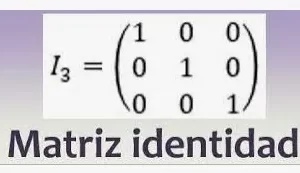
  • Función de identidad
  • Función de valor absoluto

¿Cómo determinar si una relación es una función?

Podemos comprobar si una relación es una función de forma gráfica o siguiendo los siguientes pasos.

  • Examine los valores de x o de entrada.
  • Examine también los valores de y o de salida.

Si todos los valores de entrada son diferentes, entonces la relación se convierte en una función, y si los valores se repiten, la relación no es una función.

Nota: si hay una repetición de los primeros miembros con una repetición asociada de los segundos, la relación se convierte en una función.

Ejemplo

  • Identifica el rango y el dominio de la siguiente relación:

{(-2, 3), {4, 5), (6, -5), (-2, 3)}

Solución

Como los valores de x son el dominio, la respuesta es, por tanto

⟹ {-2, 4, 6}

El rango es {-5, 3, 5}.

  • Comprueba si la siguiente relación es una función:

B = {(1, 5), (1, 5), (3, -8), (3, -8), (3, -8)}

Solución

B = {(1, 5), (1, 5), (3, -8), (3, -8), (3, -8)}

Aunque una relación no se clasifica como función si hay una repetición de valores x -, este problema es un poco complicado porque los valores x se repiten con sus correspondientes valores y.

  • Determina el dominio y el rango de la siguiente función: Z = {(1, 120), (2, 100), (3, 150), (4, 130)}.

Solución

El dominio de z = {1, 2, 3, 4 y el rango es {120, 100, 150, 130}

Vídeos de Función afín

 

Entradas Relacionadas

Matriz elemental
Matriz simétrica
Función polinómica

Entradas Relacionadas