Rectas perpendiculares

Una perpendicular es una línea recta que forma un ángulo de 90° con otra línea. El ángulo de 90° también se denomina ángulo recto y está marcado por un pequeño cuadrado entre dos líneas perpendiculares, como se muestra en la figura. En este caso, las dos rectas se cruzan en un ángulo recto y, por tanto, se dice que son perpendiculares entre sí.

Líneas perpendiculares en matemáticas

Algunas formas que tienen líneas perpendiculares son

• Cuadrado
• Triángulo rectángulo
• Rectángulo

Propiedades de la recta perpendicular

Ya hemos visto cómo son las rectas perpendiculares. Si en una figura hay una "L", el ángulo correspondiente en el vértice es un ángulo recto. Las rectas perpendiculares siempre se cruzan entre sí, sin embargo, todas las rectas que se cruzan no son siempre perpendiculares entre sí. Las dos principales propiedades de las rectas perpendiculares son:

• Las líneas perpendiculares siempre se encuentran o se intersecan entre sí.
• El ángulo entre dos rectas perpendiculares cualquiera es siempre igual a 90°.

Diferencia entre líneas paralelas y perpendiculares

Líneas paralelas

• Las líneas paralelas son aquellas que no se cruzan en ningún lugar y siempre están a la misma distancia.
• Ejemplo: los peldaños de una escalera recta; los lados opuestos de un rectángulo.
• El símbolo utilizado para denotar dos líneas paralelas: ||

Líneas perpendiculares

• Las líneas que se cruzan formando un ángulo recto se llaman líneas perpendiculares.
• Ejemplo: la esquina de dos paredes; la letra "L"
• El símbolo utilizado para denotar dos líneas perpendiculares: ⊥ .

Ejemplos de líneas perpendiculares

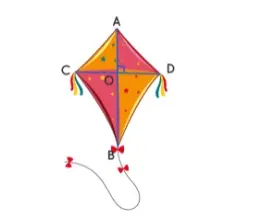
Las dos líneas del interior de la cometa se cruzan en ángulos rectos son perpendiculares. Enumera el número total de ángulos rectos que se forman en la intersección.

Solución

Como las dos rectas AB y CD se cruzan en ángulo recto, hay 4 ángulos rectos en el punto de intersección. Por lo tanto, el ángulo AOD = el ángulo DOB = el ángulo BOC = el ángulo AOC = 90°.

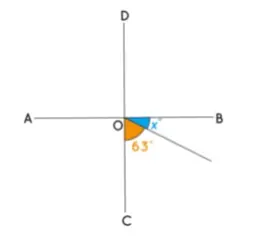
• En la siguiente figura, AB es perpendicular a CD. Si el ángulo BOC = 90°, encuentra el valor de x.

Solución

Como el ángulo BOC = 90°, podemos escribir: x + 63° = 90°. Por tanto, x = 27°

Vídeos de Rectas perpendiculares