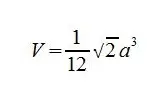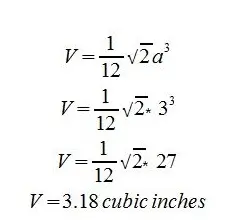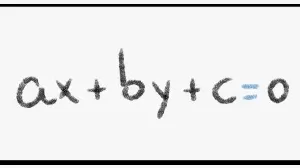Volumen de un tetraedro

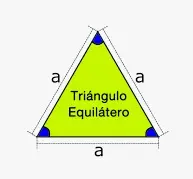
¿Y qué es esa única medida? Bueno, como el tetraedro está formado por cuatro triángulos equiláteros, todas sus aristas son iguales. Recuerda que un triángulo equilátero es un triángulo con tres lados congruentes o iguales. Así que en realidad sólo tienes un valor, y la misma medida para todas y cada una de las aristas del tetraedro. Y ésta es la única medida que necesitas para hallar el volumen y la superficie.

Para encontrar el volumen de un tetraedro, utilizarás esta fórmula:

La a representa la longitud de una de las aristas del tetraedro.

Todo lo que necesitas para encontrar el volumen es el valor de a. Una vez que tengas este número, puedes seguir adelante y enchufarlo para encontrar tu respuesta.

Por ejemplo, si el tetraedro tiene una longitud de arista de 3 pulgadas, entonces tu volumen se calcularía así

Multiplicamos todo esto y obtenemos que el volumen de este tetraedro con una arista de 3 pulgadas es de 3,18 pulgadas cúbicas.

Volumen del tetraedro

El volumen de un tetraedro se define como el espacio total que ocupa en un plano tridimensional. La fórmula para calcular el volumen del tetraedro es la siguiente

El volumen del tetraedro regular = (1/3) × área de la base × altura = (1/3) ∙ (√3)/4 ∙ a2 × (√2)/(√3) a
= (√2/12) a3 unidades cúbicas

donde a es la longitud del lado del tetraedro regular.

Ejemplo de Volumen de un tetraedro

Dos tetraedros congruentes se pegan a lo largo de su base para formar una bipirámide triangular. ¿Cuántas caras, aristas y vértices tiene esta bipirámide?

Solución:

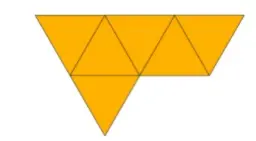
Si abrimos la bipirámide triangular para ver su red, será similar a la que se muestra en la siguiente figura:

Esto muestra que la bipirámide triangular tiene 6 caras triangulares, 9 aristas y 5 vértices.

Vídeos de Volumen de un tetraedro