Tiro parabólico horizontal

¿Qué tienen en común el agua de una fuente, una bala de cañón humana y un proyectil de artillería? Matemáticamente, todos siguen una trayectoria parabólica, que es la trayectoria que sigue un proyectil. Si te lo preguntas, un proyectil es un objeto sobre el que sólo actúa la gravedad. En matemáticas, una parábola es una curva que es la representación gráfica de una ecuación cuadrática.

Un proyectil tiene una velocidad inicial, que es horizontal o ascendente en un ángulo. Si un proyectil comenzara a ir en línea recta hacia arriba, también iría en línea recta hacia abajo. No sería una gran parábola, ya que se aplastaría en una línea recta. Lo mismo ocurriría si empezara a bajar en línea recta, o si simplemente lo dejáramos caer, así que lo que realmente vamos a ver son las trayectorias parabólicas que siguen los proyectiles con cierta velocidad inicial, o velocidad horizontal inicial.

Gravedad

La gravedad da a cada objeto en la vecindad de la Tierra una aceleración, o aumento de velocidad, de unos 32 pies por segundo cada segundo, o 32 pies/seg^2, o en unidades métricas, unos 9,81 m/seg^2. Esto significa que si dejo caer un objeto, se acelerará a medida que caiga, terminando a 32 pies por segundo al final del primer segundo, 64 pies por segundo en el segundo segundo, y así sucesivamente. Si estamos siguiendo la posición de un proyectil, hay que tener en cuenta la gravedad.

Velocidad inicial

Como mencionamos hace un momento, sólo consideraremos situaciones en las que el proyectil tiene cierta velocidad inicial. Esto significa que comienza a moverse, ya sea horizontalmente o en un ángulo. Si la velocidad inicial es estrictamente horizontal, entonces sólo necesitamos saber dónde empezó el proyectil (tal vez a nivel del suelo, tal vez muy arriba), a qué velocidad empieza a moverse y cuánto tiempo ha pasado desde que fue lanzado.

Si el proyectil apunta hacia arriba, podemos pensar que tiene una componente vertical y otra horizontal. Resulta que esto, más la gravedad, explicará todo el movimiento, y el punto de partida explicará la posición en un momento determinado.

Cómo se puede combinar todo esto

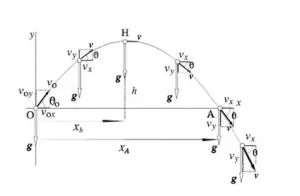
Esta imagen muestra cómo las dos componentes de la velocidad inicial y la fuerza de gravedad constante actúan sobre un proyectil. ¿Ves las flechas? La diagonal marcada con v se descompone en las componentes v sub x y v sub y. Ahora sólo vamos a ver la del principio; las otras combinan los efectos de la velocidad inicial y la gravedad.

Ahora hagamos las cuentas. Podemos establecer una ecuación para la dirección horizontal, x, y otra para la dirección vertical, y. Cualquiera de ellas dependerá del tiempo transcurrido desde el lanzamiento del proyectil, llamémoslo t y midámoslo en segundos.

En el movimiento horizontal sólo influye la componente v sub x y, por supuesto, el punto de partida. Si utilizamos la trigonometría, podemos encontrarlo a partir de v y del ángulo indicado como theta. Como se mantiene igual mientras el proyectil se mueve (no nos preocupemos por el arrastre ahora), cada segundo lo verá v sub x más lejos. Esto nos da lo siguiente

x = x sub 0 + (v sub x) * t

El movimiento vertical debido a v sub y es casi igual de sencillo, así que ocupémonos primero de esa flecha. Resulta igual que para la x. Por supuesto, empezamos con la posición original, y sub 0:

y = (v sub y) * t + y sub 0. Observa que v sub y será positiva si el proyectil comienza dirigiéndose hacia arriba y negativa si comienza dirigiéndose hacia abajo.

Ahora sólo queda la gravedad, pero siempre es la misma para todos los proyectiles (al menos en la Tierra), como ya hemos comentado. Como el proyectil sigue acelerando a medida que se dirige hacia abajo (eso es negativo, recuerda), la distancia se acumula según el cuadrado del tiempo.

Vídeos de Tiro parabólico horizontal

https://www.youtube.com/watch?v=7PHLOFylz_I