Trigonometria

Ángulo conjugado

Angulo conjugado
Los ángulos suplementarios y los ángulos complementarios se definen con respecto a la suma de dos ángulos. Si la suma de dos ángulos es de 180 grados, entonces se dice que son ángulos suplementarios, que forman juntos un ángulo recto. Mientras que si la suma de dos ángulos es de 90 grados, entonces se dice que son ángulos complementarios, y forman juntos un ángulo recto. Cuando dos segmentos de recta o líneas se encuentran en un punto común (llamado vértice), en el punto de intersección se forma un ángulo. Cuando una semirrecta gira alrededor de su punto final, la medida de su rotación en sentido contrario a las agujas del reloj es el ángulo formado entre su posición inicial y final.

Ángulo conjugado

 

Cuando la suma de dos ángulos es de 90°, entonces los ángulos se conocen como ángulos complementarios. En otras palabras, si dos ángulos se suman para formar un ángulo recto, entonces estos ángulos se denominan ángulos complementarios. Aquí decimos que los dos ángulos se complementan.

Supongamos que si un ángulo es x entonces el otro ángulo será 90o - x. Por lo tanto, usamos estos ángulos complementarios para las razones de trigonometría, donde una razón complementa a otra razón en 90 grados como;

  • sin (90°- A) = cos A y cos (90°- A) = sin A
  • tan (90°- A) = cot A y cot (90°- A) = tan A
  • sec (90°- A) = cosec A y cosec (90°- A) = sec A

Por lo tanto, se puede ver aquí la relación trigonométrica de los ángulos se cambia si se complementan entre sí.

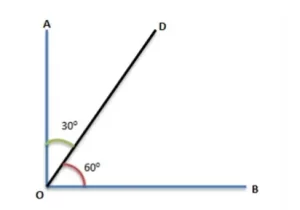
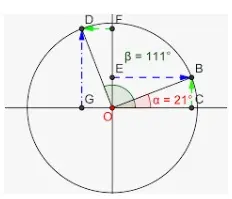
En la figura anterior, la medida del ángulo BOD es de 60o y el ángulo AOD mide 30o. Al sumar ambos ángulos obtenemos un ángulo recto, por lo que ∠BOD y ∠AOD son ángulos complementarios.

Leer  Sen 90

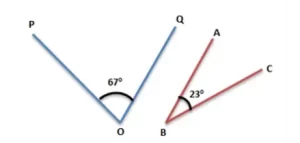
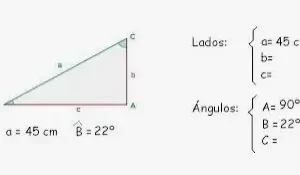
Los siguientes ángulos de la Fig. 3 dados a continuación son complementarios entre sí ya que la medida de la suma de ambos ángulos es 90o. ∠POQ y ∠ABC son complementarios y se denominan complementos entre sí.

Ángulos suplementarios

Cuando la suma de dos ángulos es de 180°, entonces los ángulos se conocen como ángulos suplementarios. En otras palabras, si dos ángulos se suman, para formar un ángulo recto, entonces esos ángulos se denominan ángulos suplementarios.

Los dos ángulos forman un ángulo lineal, tal que, si un ángulo es x, entonces el otro el ángulo es 180 - x. La linealidad aquí demuestra que las propiedades de los ángulos siguen siendo las mismas. Tomemos los ejemplos de las razones trigonométricas como

  • Sin (180 - A) = Sin A
  • Cos (180 - A) = - Cos A (se cambia el cuadrante)
  • Tan (180 - A) = - Tan A

Ejemplos resueltos de ángulos conjugados

  • Hallar el complemento de 40 grados.

Solución:

Como el ángulo dado es de 40 grados, entonces,

El complemento es 50 grados.

Sabemos que la suma de los ángulos complementarios = 90 grados

Entonces, 40° + 50° = 90°

  • Hallar el Suplemento del ángulo 1/3 de 210°.

Solución:

Paso 1: Convertir 1/3 de 210°

Es decir, 1/3 x 210° = 70°

Paso 2: Suplemento de 70° = 180° - 70° = 110°

Por lo tanto, el suplemento del ángulo 1/3 de 210° es 110°.

Vídeos de Ángulo conjugado

Entradas Relacionadas

Calcular ángulos de un triangulo
Trigonometría
Ángulo suma

Contenido

Entradas Relacionadas