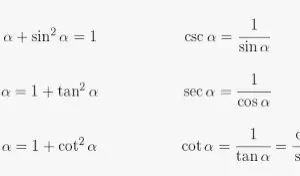Razones trigonométricas recíprocas

Los recíprocos de las seis funciones trigonométricas fundamentales (seno, coseno, tangente, secante, cosecante y cotangente) se llaman identidades recíprocas. Las identidades recíprocas son importantes identidades trigonométricas que se utilizan para resolver diversos problemas de trigonometría. Cada función trigonométrica es recíproca de otra función trigonométrica. La función seno es la recíproca de la función cosecante y viceversa; la función coseno es la recíproca de la función secante y viceversa; la función cotangente es la recíproca de la función tangente y viceversa.

Fórmulas de identidades recíprocas

Las identidades recíprocas se aplican en varios problemas de trigonometría para simplificar los cálculos. Las fórmulas de las seis principales identidades recíprocas son

sen x = 1/cosec x
cos x = 1/seg x
tan x = 1/cot x
cot x = 1/tan x
sec x = 1/cos x
cosec x = 1/sin x

Demostración de las identidades recíprocas

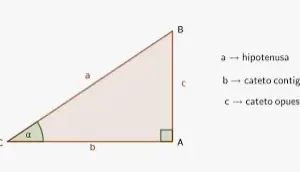
Ahora que conocemos las identidades recíprocas de la trigonometría, vamos a demostrar cada una de ellas utilizando la definición de las funciones trigonométricas básicas. En primer lugar, derivaremos la identidad recíproca de la función seno. Consideremos un triángulo rectángulo ABC con un ángulo recto en C.

Sabemos que sin θ = Perpendicular/Hipotenusa = c/a y cosec θ = Hipotenusa/Perpendicular = a/c ⇒ sin θ es el recíproco de cosec θ y cosec θ es el recíproco de sin θ. Del mismo modo, demostraremos otras identidades recíprocas. cos θ = Base/Hipotenusa = b/a y cosec θ = Hipotenusa/Base = a/b ⇒ cos θ es el recíproco de sec θ y sec θ es el recíproco de cos θ. tan θ = sin θ/cos θ y cot θ = cos θ/sin θ ⇒ tan θ es el recíproco de cot θ y cot θ es el recíproco de tan θ. Por tanto, tenemos

sin θ es el recíproco de cosec θ
cosec θ es el recíproco de sin θ
cos θ es el recíproco de sec θ
sec θ es el recíproco de cos θ
tan θ es el recíproco de cot θ
cot θ es el recíproco de tan θ

Vídeos de Razones trigonométricas recíprocas